题目内容
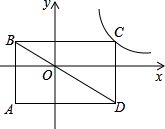如图，矩形ABCD的边平行于坐标轴，对角线BD经过坐标原点，点C在反比例函数y=| k |
| x |
| A、2 | B、4 | C、8 | D、16 |
考点：反比例函数图象上点的坐标特征,矩形的性质
专题：计算题
分析：根据矩形的性质得到S△OBF=S△OGB，S△OED=S△ODH，则S矩形AEOF=S矩形CHOG=4，然后根据反比例函数比例系数的几何意义求解．
解答：
解：如图，
∵四边形ABCD为矩形，对角线BD经过坐标原点，
∴S△OBF=S△OGB，S△OED=S△ODH，
∴S矩形AEOF=S矩形CHOG，
而A（-2，-2），
∴S矩形CHOG=S矩形AEOF=2×2=4，
∴k=4．
故选B．
解：如图，∵四边形ABCD为矩形，对角线BD经过坐标原点，
∴S△OBF=S△OGB，S△OED=S△ODH，
∴S矩形AEOF=S矩形CHOG，
而A（-2，-2），
∴S矩形CHOG=S矩形AEOF=2×2=4，
∴k=4．
故选B．
点评：本题考查了反比例函数图象上点的坐标特征：反比例函数y=
（k为常数，k≠0）的图象是双曲线；图象上的点（x，y）的横纵坐标的积是定值k，即xy=k．也考查了矩形的性质．
| k |
| x |
练习册系列答案
阅读快车系列答案
相关题目
已知反比例函数y=
的图象经过点（m，3m），则此反比例函数的图象在（ ）
| k |
| x |
| A、第一、二象限 |
| B、第一、三象限 |
| C、第二、四象限 |
| D、第三、四象限 |
先向右平移1个单位，再向上平移3个单位，则平移后抛物线的解析式为（ ）
B．
D．
＝ ．
的图象顶点在x轴上，则a＝ ．
的图象如图所示，则下面四个结论中正确的结论有（ ）
= ．