题目内容
⊙O的直径为10，圆心O到弦AB的距离OM的长为3，则弦AB的长是（ ）
| A．4 | B．6 | C．7 | D．8 |
D．
解析试题分析：先根据垂径定理求出AM=
AB，再根据勾股定理求出AM的值．
试题解析：连接OA，
∵⊙O的直径为10，
∴OA=5，
∵圆心O到弦AB的距离OM的长为3，
由垂径定理知，点M是AB的中点，AM=AB，
由勾股定理可得，AM=4，所以AB=8．
故选D．
考点：1.垂径定理；2.勾股定理．
练习册系列答案
阅读快车系列答案
相关题目
，其中
，
.
与
互为相反数，那么a=___________如图，从边长为（a+1）cm的正方形纸片中剪去一个边长为（a﹣1）cm的正方形（a＞1），剩余部分沿虚线又剪拼成一个矩形（不重叠无缝隙），则该矩形的面积是（ ）
| A．2cm2 | B．2acm2 | C．4acm2 | D．（a2﹣1）cm2 |
如图，DC 是⊙O直径，弦AB⊥CD于F，连接BC，DB，则下列结论错误的是（ ）
A． | B．AF=BF | C．OF=CF | D．∠DBC=90° |
，那么
的度数是（ ）
如图,A,B,C是☉O上的三点,且∠ABC=70°,则∠AOC的度数是（ ）
| A．35° | B．140° | C．70° | D．70°或140° |
与⊙O相切于点C，过点A作AD⊥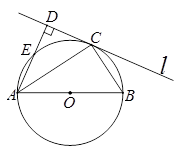
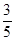，BC＝6，求DE的长．
的图象在其所在的每一象限内，函数值y随自变量x的增大而增大，则m的取值范围是（ ）
B．
C．
D．