Question

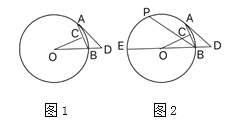
【题目】如图1，在圆中，垂直于弦，为垂足，作，与的延长线交于.

（1）求证：是圆的切线；

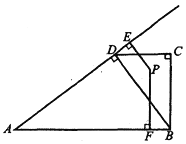
（2）如图2，延长，交圆于点，点是劣弧的中点，，，求的长 .

Answer 1

【答案】（1）详见解析；（2）

【解析】

（1）连接OA，利用切线的判定证明即可；
（2）分别连结OP、PE、AE，OP交AE于F点，根据勾股定理解答即可．

解：（1）如图，连结OA，

∵OA=OB，OC⊥AB，
∴∠AOC=∠BOC，
又∠BAD=∠BOC，
∴∠BAD=∠AOC
∵∠AOC+∠OAC=90°，
∴∠BAD+∠OAC=90°，
∴OA⊥AD，
即：直线AD是⊙O的切线；
（2）分别连结OP、PE、AE，OP交AE于F点，
∵BE是直径，
∴∠EAB=90°，
∴OC∥AE，
∵OB=，
∴BE=13
∵AB=5，在直角△ABE中，AE=12，EF=6，FP=OP-OF=-=4
在直角△PEF中，FP=4，EF=6，PE2=16+36=52，
在直角△PEB中，BE=13，PB2=BE2-PE2，
PB=＝3．