题目内容
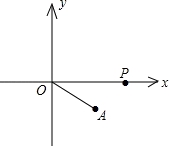
如图,直线a、b相交于点A,C、E分别是直线b、a上两点且BC⊥a,DE⊥b,点M、N是EC、DB的中点.求证:MN⊥BD.

【考点】直角三角形斜边上的中线;等腰三角形的判定与性质.
【专题】证明题.
【分析】根据直角三角形斜边上的中线等于斜边的一半可得DM= EC,BM=
EC,BM= EC,从而得到DM=BM,再根据等腰三角形三线合一的性质证明.
EC,从而得到DM=BM,再根据等腰三角形三线合一的性质证明.
【解答】证明 :∵BC⊥a,DE⊥b,点M是EC的中点,
:∵BC⊥a,DE⊥b,点M是EC的中点,
∴DM= EC,BM=
EC,BM= EC,
EC,
∴DM=BM,
∵点N是BD的中点,
∴MN ⊥BD.
⊥BD.
【点评】本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形三线合一的性质,熟记性质并准确识图是解题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目

 每天各能铺设多少米?
每天各能铺设多少米?
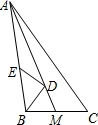
 点P的个数为( )
点P的个数为( )