题目内容
18.化简:$\frac{x-y}{\sqrt{x}+\sqrt{y}}$-$\frac{x+y-2\sqrt{xy}}{\sqrt{x}-\sqrt{y}}$(x>y).分析 利用二次根式的性质和平方差、完全平方公式得到原式=$\frac{(\sqrt{x}+\sqrt{y})(\sqrt{x}-\sqrt{y})}{\sqrt{x}+\sqrt{y}}$-$\frac{(\sqrt{x}-\sqrt{y})^{2}}{\sqrt{x}-\sqrt{y}}$,然后约分后合并即可.
解答 解:原式=$\frac{(\sqrt{x}+\sqrt{y})(\sqrt{x}-\sqrt{y})}{\sqrt{x}+\sqrt{y}}$-$\frac{(\sqrt{x}-\sqrt{y})^{2}}{\sqrt{x}-\sqrt{y}}$
=$\sqrt{x}$-$\sqrt{y}$-($\sqrt{x}$-$\sqrt{y}$)
=0.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.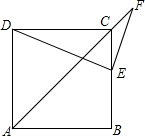 如图,正方形ABCD的边长为10+5$\sqrt{2}$,点E在边CB上,点F在AC的延长线上,EF⊥DE.若CE=CF,则CE的值为( )
如图,正方形ABCD的边长为10+5$\sqrt{2}$,点E在边CB上,点F在AC的延长线上,EF⊥DE.若CE=CF,则CE的值为( )
 如图,正方形ABCD的边长为10+5$\sqrt{2}$,点E在边CB上,点F在AC的延长线上,EF⊥DE.若CE=CF,则CE的值为( )
如图,正方形ABCD的边长为10+5$\sqrt{2}$,点E在边CB上,点F在AC的延长线上,EF⊥DE.若CE=CF,则CE的值为( )| A. | 5 | B. | 5$\sqrt{2}$ | C. | 10 | D. | 10$\sqrt{2}$ |
 如图,平面直角坐标系中,直线AB与x轴,y轴分别交于A(3,0),B(0,$\sqrt{3}$)两点,点C、D分别为线段AB、OA上的一动点.
如图,平面直角坐标系中,直线AB与x轴,y轴分别交于A(3,0),B(0,$\sqrt{3}$)两点,点C、D分别为线段AB、OA上的一动点.