题目内容
12.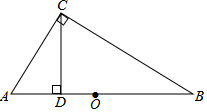 如图,在△ABC中,∠ACB=90°,AB=10,BC=8,CD⊥AB于点D,O为AB的中点.
如图,在△ABC中,∠ACB=90°,AB=10,BC=8,CD⊥AB于点D,O为AB的中点.(1)以C为圆心,6为半径作圆,试判断点A,D,B与⊙C的位置关系.
(2)当⊙C的半径为多少时,点O在⊙C上.
(3)若以点C为圆心作圆,使A、O、B三点至少有一点在圆内,至少有一点在圆外,则⊙C的半径r的取值范围是什么?
分析 (1)各点到C的距离与半径6作对比,大于半径的在圆外,等于半径的在圆上,小于半径的在圆内;
(2)根据直角三角形斜边中线等于斜边一半得OC=5,所以当半径为5时,O在⊙C上;
(3)对比OC<AC<BC,确定O在圆内,B在圆外,写出半径r的取值即可.
解答 解:(1)如图,在△ABC中,∠ACB=90°,AB=10,BC=8,
∴AC=6,
∴A在⊙C上,
∵CD⊥AB,
∴S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•CD,
6×8=10CD,
CD=4.8<6,
∴D在⊙C内,
∵BC=8>6,
∴B在⊙C外;
(2)在△ABC中,∠ACB=90°,
∵O为AB的中点,
∴OC=$\frac{1}{2}$AB=5,
∴当⊙C的半径为5时,点O在⊙C上;
(3)∵AC=6,OC=5,BC=8,
∴OC<AC<BC,
∴当5<r<8时,A、O、B三点至少有一点在圆内,至少有一点在圆外,
点评 此题主要考查了点与圆的位置关系、直角三角形斜边上的中线的性质、勾股定理,解决本题要注意点与圆的位置关系,要熟悉勾股定理,及点与圆的位置关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.下列数字中,属于最简二次根式的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{\frac{2}{3}}$ | C. | $\sqrt{7}$ | D. | $\sqrt{0.3}$ |
20.下列事件是必然事件的是( )
| A. | 经过不断的努力,每个人都能获得“星光大道”年度总冠军 | |
| B. | 小冉打开电视,正在播放“奔跑吧,兄弟” | |
| C. | 火车开到月球上 | |
| D. | 在十三名中国学生中,必有属相相同的 |
7.9的平方根是( )
| A. | ±3 | B. | -3 | C. | 3 | D. | $±\frac{1}{3}$ |
17.不等式x-2≤0的解集在数轴上表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
4.化简-b•b3•b4的正确结果是( )
| A. | -b7 | B. | b7 | C. | -b8 | D. | b8 |
1.下列运算正确的是( )
| A. | (ab)2=a2b2 | B. | a2+a4=a6 | C. | (a2)3=a5 | D. | a2•a3=a6 |
2.已知x,y为实数.且$\sqrt{x-1}$+3(2-y)2=0.则x-y的值是( )
| A. | 3 | B. | -3 | C. | 1 | D. | -1 |
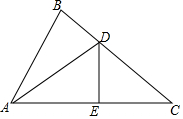 如图,已知∠BAC=60°,∠B=80°,DE垂直平分AC交BC于点D,交AC于E.
如图,已知∠BAC=60°,∠B=80°,DE垂直平分AC交BC于点D,交AC于E.