题目内容
2. 如图,AB⊥OD,∠BOC比∠DOC大34°,OE平分∠AOC,求:
如图,AB⊥OD,∠BOC比∠DOC大34°,OE平分∠AOC,求:(1)∠COD的大小;
(2)∠DOE的大小.
分析 (1)结合已知设∠DOC=x°,则∠BOC=x°+34°,再利用垂直的定义得出答案;
(2)利用(1)中所求,结合角平分线的性质求出答案.
解答 解:(1)由题意可得:设∠DOC=x°,则∠BOC=x°+34°,
∵AB⊥OD,
∴∠DOC+∠BOC=90°,
则x°+x°+34°=90°,
解得:x=28.
故∠COD的度数为28°;
(2)∵∠AOD=90°,∠DOC=34°,
∴∠AOC=124°,
∵OE平分∠AOC,
∴∠EOC=∠AOE=62°,
∴∠DOE的度数为:∠EOC-∠DOC=62°-28°=34°.
点评 此题主要考查了垂直的定义以及角平分线的性质,正确得出∠AOC的度数是解题关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
17.若一元二次方程(1-2k)x2+8x-6=0没有实数根,那么k的最小值是( )
| A. | 2 | B. | 0 | C. | 1 | D. | 3 |
11.一个不透明的盒子中装有3个白球,5个红球和7个黄球,这些球除颜色外,没有任何其他区别,现从这个盒子中随机摸出一个球,摸到红球的可能性是( )
| A. | $\frac{7}{15}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{15}$ |
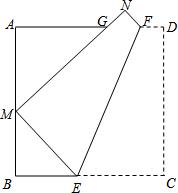 如图,折叠边长为a的正方形ABCD,使点C落在边AB上的点M处(不与点A,B重合),点D落在点N处,折痕EF分别与边BC、AD交于点E、F,MN与边AD交于点G.证明:
如图,折叠边长为a的正方形ABCD,使点C落在边AB上的点M处(不与点A,B重合),点D落在点N处,折痕EF分别与边BC、AD交于点E、F,MN与边AD交于点G.证明: 如图,已知平面直角坐标系中,直线y=$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点B,与直线y=x交于点C.
如图,已知平面直角坐标系中,直线y=$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点B,与直线y=x交于点C.