题目内容
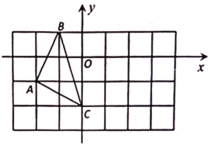
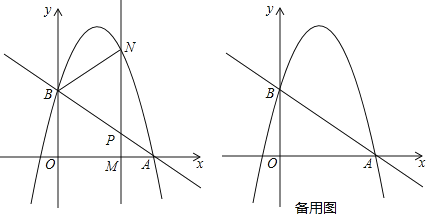
【题目】如图,直线y=kx+2与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣![]() x2+bx+c经过点A,B.
x2+bx+c经过点A,B.
(1)求k的值和抛物线的解析式.
(2)M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N,连接BN.
①若△BPN是直角三角形,求点N的坐标.
②当∠PBN=45°时,请直接写出m的值.(注:当k1k2=﹣1时,直线y=k1x+b1与直线y=k2x+b2垂直)
【答案】(1)k=﹣![]() , y=﹣
, y=﹣![]() x2+
x2+![]() x+2;(2)①点N(
x+2;(2)①点N(![]() ,
,![]() );②m=
);②m=![]() 或m=
或m=![]()
【解析】
(1)把![]() 点坐标代入直线解析式可求得
点坐标代入直线解析式可求得![]() ,则可求得
,则可求得![]() 点坐标,由
点坐标,由![]() 、
、![]() 的坐标,利用待定系数法可求得抛物线解析式;
的坐标,利用待定系数法可求得抛物线解析式;
(2)①分![]() 和
和![]() 两种情况讨论,即可求解;
两种情况讨论,即可求解;
②有两解,![]() 点在
点在![]() 的上方或下方,作辅助线,构建等腰直角三角形,由
的上方或下方,作辅助线,构建等腰直角三角形,由![]() 得
得![]() ,设
,设![]() ,则由
,则由![]() ,得
,得![]() ,
,![]() ,根据
,根据![]() ,可得
,可得![]() 和
和![]() 的解析式,分别与抛物线联立方程组,可得结论.
的解析式,分别与抛物线联立方程组,可得结论.
解:(1)把![]() 代入
代入![]() 中得,
中得,![]() ,
,
![]() ,
,
![]() 直线
直线![]() 的解析式为:
的解析式为:![]() ,
,
![]() ,
,
把![]() 和
和![]() 代入抛物线
代入抛物线![]() 中,
中,
则![]() ,
,
解得: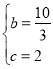 ,
,
二次函数的表达式为:![]() ;
;
(2)①当![]() 时,且
时,且![]() ,
,
![]() ,
,
![]() ,
,
![]() 点
点![]() 的纵坐标为2,
的纵坐标为2,
![]() ,
,
![]() (舍去),
(舍去),![]() ,
,
![]() 点
点![]() 坐标
坐标![]() ,
,![]() ;
;
当![]() 时,
时,
直线![]() 的解析式为:
的解析式为:![]() ,
,
![]()
![]() ,
,
![]() (舍去),
(舍去),![]() ,
,
![]() 点N(
点N(![]() ,
,![]() );
);
②有两解,![]() 点在
点在![]() 的上方或下方,
的上方或下方,
如图2,过点![]() 作
作![]() 的垂线交
的垂线交![]() 轴于点
轴于点![]() ,
,
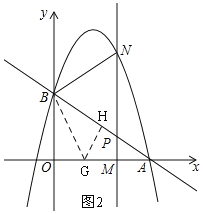
过点![]() 作
作![]() 的垂线,垂足为点
的垂线,垂足为点![]() .
.
由![]() 得
得![]() ,
,
![]() ,
,
设![]() ,则由
,则由![]() ,
,
![]()
![]() ,
,
得![]() ,
,![]() ,
,
由![]() ,解得
,解得![]() ,
,
![]() ,
,
从而![]() ,
,
即![]() ,
,![]() ,
,
由![]() ,
,![]() ,
,![]() 得:
得:
直线![]() ,直线
,直线![]() .
.
则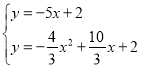 ,
,
解得:![]() (舍),
(舍),![]() ,
,
即![]() ;
;
则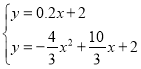 ,
,
解得:![]() (舍
(舍![]() ,
,![]() ;
;
即![]() ;
;
故![]() 与
与![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目