题目内容
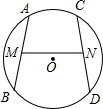如图，AB、CD是⊙O的弦，M、N分别为AB、CD的中点，且∠AMN=∠CNM．求证：AB=CD．
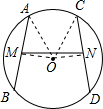证明：连接OM，ON，OA，OC，∵M、N分别为AB、CD的中点，
∴OM⊥AB，ON⊥CD，
∴AM=
AB，CN=CD，∵∠AMN=∠CNM，
∴∠NMO=∠MNO，即OM=ON，
在Rt△AOM与Rt△CON中，
∵
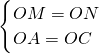，∴Rt△AOM≌Rt△CON（HL），
∴AM=CN，
∴AB=CD．
分析：连接OM，ON，OA，OC，先根据垂径定理得出AM=
AB，CN=CD，再由∠AMN=∠CNM得出∠NMO=∠MNO，即OM=ON，再由OA=OC可知Rt△AOM≌Rt△CON，故AM=CN，由此即可得出结论．点评：本题考查的是垂径定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
相关题目
21、如图，AB、CD是⊙O的弦，∠A=∠C．求证：AB=CD．
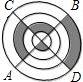如图，AB、CD是水平放置的轮盘（俯视图）上两条互相垂直的直径，一个小钢球在轮盘上自由滚动，该小钢球最终停在阴影区域的概率为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
（2013•泰安）如图，AB，CD是⊙O的两条互相垂直的直径，点O1，O2，O3，O4分别是OA、OB、OC、OD的中点，若⊙O的半径为2，则阴影部分的面积为（ ）
（2013•盘锦）如图，AB，CD是⊙O的直径，点E在AB延长线上，FE⊥AB，BE=EF=2，FE的延长线交CD延长线于点G，DG=GE=3，连接FD．
如图，AB，CD是⊙O的两条弦，且AB=CD，点M是