题目内容
如图,它们是用一系列的正方形组合的图形,且图中的三角形都是等腰三角形,第①个图形中的正方形边长是
;第②个图形中最大的一个正方形的边长为2,;第③个图形中最大的一个正方形的边长为2
;按如此规律,第⑧个图形中最大的一个正方形的边长是( )

| 2 |
| 2 |

| A、8 | ||
| B、16 | ||
C、4
| ||
D、8
|
考点:正方形的性质
专题:规律型
分析:根据图形中数据得出1=(
)0,
=(
)1,2=(
)2,即可得出正方形的边长变化规律求出即可.
| 2 |
| 2 |
| 2 |
| 2 |
解答:解:∵第①个图形中的正方形边长是1=(
)0;
第②个图形中最大的一个正方形的边长为
=(
)1;
第③个图形中最大的一个正方形的边长为2=(
)2;
∴按照此规律,第⑧个图形中最大的一个正方形的边长是:(
)7=8
.
故选:D.
| 2 |
第②个图形中最大的一个正方形的边长为
| 2 |
| 2 |
第③个图形中最大的一个正方形的边长为2=(
| 2 |
∴按照此规律,第⑧个图形中最大的一个正方形的边长是:(
| 2 |
| 2 |
故选:D.
点评:此题主要考查了图形的变化类以及正方形的性质,根据已知得出边长的变化规律是解题关键.

练习册系列答案
相关题目
看表,则相应的代数式是( )
| x | 0 | 1 | 2 | 3 |
| 代数式值 | 2 | -1 | -4 | -7 |
| A、x+2 | B、2x-3 |
| C、3x-1 | D、-3x+2 |
下列不是二次函数的是( )
| A、y=3(x-1)2-1 | ||
B、y=
| ||
C、y=
| ||
| D、y=(x+1)(x-1) |
如果2是一元二次方程x2+kx+2=0的一个根,那么常数k的值是( )
| A、2 | B、-2 | C、3 | D、-3 |
下列说法中正确的是( )
| A、一个角的补角一定是钝角 |
| B、若∠A+∠B+∠C=90°,则∠A+∠B是∠C的余角 |
| C、互补的两个角不可能相等 |
| D、∠A的补角与∠A的余角的差一定等于直角 |
下列说法正确的是( )
| A、无理数就是开方开不尽的数 |
| B、无理数是无限不循环小数 |
| C、带根号的数都是无理数 |
| D、无限小数都是无理数 |
整式5m2-3m-5减去整式-3m所得的结果是( )
| A、5(m2-1) |
| B、5m2-6m-5 |
| C、5(m2+1) |
| D、-(5m2+6m-5) |
下列结论正确的是( )
| A、64的立方根是±4 | ||||||
B、-
| ||||||
| C、立方根等于本身的数是0 | ||||||
D、
|
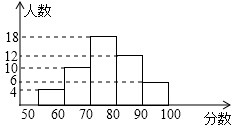 某班进行数学测验,将所得成绩(得分取整数)进行整理后分成5组,并绘制成频数分布直方图,请你结合直方图所提供的信息,回答下列问题:
某班进行数学测验,将所得成绩(得分取整数)进行整理后分成5组,并绘制成频数分布直方图,请你结合直方图所提供的信息,回答下列问题: