题目内容
如图，A、D是⊙O上的两个点，BC是直径，若∠D=36°，则∠OAC的度数是________．
54°
分析：在同圆和等圆中，同弧所对的圆心角是圆周角的2倍，所以∠AOC=2∠D=72°，而△AOC中，AO=CO，所以∠OAC=∠OCA，而180°-∠AOC=108°，所以∠OAC=54°．
解答：∵∠D=36°，
∴∠AOC=2∠D=72°，
∴∠OAC=（180°-∠AOC）÷2=108°÷2=54°．
故答案为：54°．
点评：本题考查同弧所对的圆周角和圆心角的关系．规律总结：解决与圆有关的角度的相关计算时，一般先判断角是圆周角还是圆心角，再转化成同弧所对的圆周角或圆心角，利用同弧所对的圆周角相等，同弧所对的圆周角是圆心角的一半等关系求解．特别地，当有直径这一条件时，往往要用到直径所对的圆周角是直角这一条件．
分析：在同圆和等圆中，同弧所对的圆心角是圆周角的2倍，所以∠AOC=2∠D=72°，而△AOC中，AO=CO，所以∠OAC=∠OCA，而180°-∠AOC=108°，所以∠OAC=54°．
解答：∵∠D=36°，
∴∠AOC=2∠D=72°，
∴∠OAC=（180°-∠AOC）÷2=108°÷2=54°．
故答案为：54°．
点评：本题考查同弧所对的圆周角和圆心角的关系．规律总结：解决与圆有关的角度的相关计算时，一般先判断角是圆周角还是圆心角，再转化成同弧所对的圆周角或圆心角，利用同弧所对的圆周角相等，同弧所对的圆周角是圆心角的一半等关系求解．特别地，当有直径这一条件时，往往要用到直径所对的圆周角是直角这一条件．
练习册系列答案
教材全解字词句篇系列答案
相关题目
如图，A、D是⊙O上的两个点，BC是直径，若∠D=35°，则∠OAC等于（ ）| A、65° | B、35° | C、70° | D、55° |
20、已知：如图，E、F是AB上的两点，AE=BF，AC∥BD，∠C=∠D．求证：CF=DE．
如图，A、B是⊙O上的两点，AC是⊙O的切线，∠OBA=75°，⊙O的半径为1，则OC的长等于（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
（2012•南京）如图，A、B是⊙O上的两个定点，P是⊙O上的动点（P不与A、B重合）、我们称∠APB是⊙O上关于点A、B的滑动角．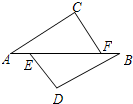
已知：如图，E、F是AB上的两点，AC=BD，AC∥BD，∠C=∠D；