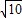题目内容
在△ABC中,最大角∠A是最小角∠C的2倍,且AB=2,AC=3,则△ABC的周长为
- A.12-

- B.7
 -
-
- C.5+2

- D.5+

D
分析:作出图形,作△ABC的角平分线AD交BC于D,根据角平分线的定义可得∠BAD=∠CAD= ∠BAC,然后求出∠BAD=∠C=∠CAD,根据等角对等边可得AD=CD,根据两角对应相等两三角形相似可得△ABC和△DBA相似,根据相似三角形对应边成比例可得
∠BAC,然后求出∠BAD=∠C=∠CAD,根据等角对等边可得AD=CD,根据两角对应相等两三角形相似可得△ABC和△DBA相似,根据相似三角形对应边成比例可得 =
= =
= ,然后代入数据求出BC的长,再根据三角形的周长定义列式计算即可得解.
,然后代入数据求出BC的长,再根据三角形的周长定义列式计算即可得解.
解答: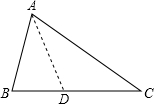 解:如图,作△ABC的角平分线AD交BC于D,
解:如图,作△ABC的角平分线AD交BC于D,
则∠BAD=∠CAD= ∠BAC,
∠BAC,
∵最大角∠A是最小角∠C的2倍,
∴∠C= ∠BAC,
∠BAC,
∴∠BAD=∠C=∠CAD,
∴AD=CD,
又∵∠B=∠B,
∴△ABC∽△DBA,
∴ =
= =
= ,
,
∵AB=2,AC=3,
∴ =
= =
=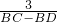 ,
,
∴BD•BC=4①,
3BD=2BC-2BD②,
由②得,BD= BC③,
BC③,
③代入①得, BC•BC=4,
BC•BC=4,
解得BC= ,
,
∴△ABC的周长=AB+BC+AC=2+ +3=5+
+3=5+ .
.
故选D.
点评:本题考查了相似三角形的判定与性质,作辅助线构造出相似三角形,然后根据相似三角形对应边成比例得到两个等式并整理成关于BC的方程是解题的关键,也是本题的难点,作出图形更形象直观.
分析:作出图形,作△ABC的角平分线AD交BC于D,根据角平分线的定义可得∠BAD=∠CAD=
 ∠BAC,然后求出∠BAD=∠C=∠CAD,根据等角对等边可得AD=CD,根据两角对应相等两三角形相似可得△ABC和△DBA相似,根据相似三角形对应边成比例可得
∠BAC,然后求出∠BAD=∠C=∠CAD,根据等角对等边可得AD=CD,根据两角对应相等两三角形相似可得△ABC和△DBA相似,根据相似三角形对应边成比例可得 =
= =
= ,然后代入数据求出BC的长,再根据三角形的周长定义列式计算即可得解.
,然后代入数据求出BC的长,再根据三角形的周长定义列式计算即可得解.解答:
 解:如图,作△ABC的角平分线AD交BC于D,
解:如图,作△ABC的角平分线AD交BC于D,则∠BAD=∠CAD=
 ∠BAC,
∠BAC,∵最大角∠A是最小角∠C的2倍,
∴∠C=
 ∠BAC,
∠BAC,∴∠BAD=∠C=∠CAD,
∴AD=CD,
又∵∠B=∠B,
∴△ABC∽△DBA,
∴
 =
= =
= ,
,∵AB=2,AC=3,
∴
 =
= =
=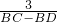 ,
,∴BD•BC=4①,
3BD=2BC-2BD②,
由②得,BD=
 BC③,
BC③,③代入①得,
 BC•BC=4,
BC•BC=4,解得BC=
 ,
,∴△ABC的周长=AB+BC+AC=2+
 +3=5+
+3=5+ .
.故选D.
点评:本题考查了相似三角形的判定与性质,作辅助线构造出相似三角形,然后根据相似三角形对应边成比例得到两个等式并整理成关于BC的方程是解题的关键,也是本题的难点,作出图形更形象直观.

练习册系列答案
相关题目


 -
-