题目内容
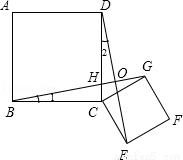
(11分)如图,四边形ABCD是正方形,以CG为一边在正方形ABCD外作正方形CEFG,连结BG,DE,猜想如图中线段BG、线段DE的关系并证明.

详见解析
【解析】
试题分析:由于四边形ABCD、四边形CEFG是正方形,那么又BC=CD,CG=CF,∠BCD=∠GCE=90°,利用等式性质有∠BCD+∠DCG=∠GCE+∠DCG,即∠BCG=∠DCE,利用SAS可证△BCG≌△DCE,那么有BG=DE,∠1=∠2,又∵∠BHC=∠DHO,于是可得∠1+∠BHC=∠2+∠DHO,即∠2+∠DHO=90°,结合三角形内角和定理可得∠DOH=90°,从而BG⊥DE.
试题解析:猜想:BG=DE,且BG⊥DE.
证明:如右图所示,
∵四边形ABCD、四边形CEFG是正方形,
∴∠BCD=∠GCE=90°,BC=CD,CE=CG,
∴∠BCD+∠DCG=∠GCF+∠DCG,
即∠BCG=∠DCE,
∴△BCG≌△DCE,
∴∠1=∠2,BG=DE,
又∵∠BHC=∠DHO,
∴∠1+∠BHC=∠2+∠DHO,
即∠2+∠DHO=90°,
∴∠DOH=180°﹣90°=90°,
∴BG⊥DE.
考点:1.正方形的性质;2.全等三角形的判定与性质.
考点分析: 考点1:四边形 四边形:四边形的初中数学中考中的重点内容之一,分值一般为10-14分,题型以选择,填空,解答证明或融合在综合题目中为主,难易度为中。主要考察内容:①多边形的内角和,外角和等问题②图形的镶嵌问题③平行四边形,矩形,菱形,正方形,等腰梯形的性质和判定。突破方法:①掌握多边形,四边形的性质和判定方法。熟记各项公式。②注意利用四边形的性质进行有关四边形的证明。③注意开放性题目的解答,多种情况分析。 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 在实数范围内有意义,则
在实数范围内有意义,则 的取值范围是( )
的取值范围是( ) B、
B、 C、
C、 D、
D、
 -2x+1=0有两个不相等的实数根,则a的取值范围是( )
-2x+1=0有两个不相等的实数根,则a的取值范围是( )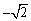 ,
,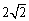 ,a,b,其中a,b是方程
,a,b,其中a,b是方程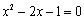 的两个根,则这4个数据的中位数是( )
的两个根,则这4个数据的中位数是( ) 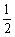 C.2 D.
C.2 D.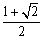

 ,则菱形较小的内角的度数为 .
,则菱形较小的内角的度数为 .