题目内容
如图,已知菱形ABCD的两条对角线分别是6和8,M、N分别是BC、CD的中点,点P是对角线BD上一点,则PM+PN的最小值是________.

5
【解析】
试题分析:作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP的值最小,连接AC,求出CP、PB,根据勾股定理求出BC长,证出MP+NP=QN=BC,即可得出答案.
作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP的值最小,连接AC,
∵四边形ABCD是菱形,
∴AC⊥BD,∠QBP=∠MBP,
即Q在AB上,
∵MQ⊥BD,
∴AC∥MQ,
∵M为BC中点,
∴Q为AB中点,
∵N为CD中点,四边形ABCD是菱形,
∴BQ∥CD,BQ=CN,
∴四边形BQNC是平行四边形,
∴NQ=BC,
∵四边形ABCD是菱形,
∴CP= AC=3,BP=
AC=3,BP= BD=4,
BD=4,
在Rt△BPC中,由勾股定理得:BC=5,
即NQ=5,
∴MP+NP=QP+NP=QN=5,
故答案为:5

考点:1. 轴对称-最短路线问题;2.菱形的性质.
考点分析: 考点1:四边形 四边形:四边形的初中数学中考中的重点内容之一,分值一般为10-14分,题型以选择,填空,解答证明或融合在综合题目中为主,难易度为中。主要考察内容:①多边形的内角和,外角和等问题②图形的镶嵌问题③平行四边形,矩形,菱形,正方形,等腰梯形的性质和判定。突破方法:①掌握多边形,四边形的性质和判定方法。熟记各项公式。②注意利用四边形的性质进行有关四边形的证明。③注意开放性题目的解答,多种情况分析。 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目

 的方程
的方程 是一元二次方程,则
是一元二次方程,则 .
.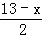 =20
=20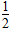 x ) =20 D、x·
x ) =20 D、x·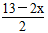 =20
=20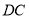 ,DC2=DE·DA是否成立?若成立,给出证明;若不成立,举例说明.
,DC2=DE·DA是否成立?若成立,给出证明;若不成立,举例说明.