��Ŀ����
10��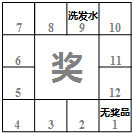 ���̳���Ϊ�������˿ͣ�������һ���齱�����ͼ������˿͵�Ʊ��ÿ�Σ�������100Ԫ�����ܻ��һ�γ齱���ᣬ�Ұٷ�֮���н����˿�ͬʱ���������ӣ����ֳ��ϵĵ���֮���Ǽ������ܻ����Ӧ���ָ����е���Ʒ��
���̳���Ϊ�������˿ͣ�������һ���齱�����ͼ������˿͵�Ʊ��ÿ�Σ�������100Ԫ�����ܻ��һ�γ齱���ᣬ�Ұٷ�֮���н����˿�ͬʱ���������ӣ����ֳ��ϵĵ���֮���Ǽ������ܻ����Ӧ���ָ����е���Ʒ����1�������ֵ�һλ�˿ͳ齱�����û���״ͼ���б��ķ�����ʾ��λ�˿͵õ�ϴ��ˮ�ĸ����Ƕ��٣�
��2������˵��������ƭ��Ϊ������1��Ӧ�ĸ���û�н�Ʒ����˲���˵�ٷ�֮���н�������˵����ȷ��Ϊʲô��
���� ��1������״ͼչʾ����36�ֵȿ��ܵĽ�����ҳ�����֮��Ϊ9�ļ�������Ȼ����ݸ��ʹ�ʽ��⣻
��2�����������ӣ����ֳ��ϵĵ���֮����СΪ2�����ǿ��жϳ��в�������ƭ��Ϊ��
��� �⣺��1������״ͼΪ��
����36�ֵȿ��ܵĽ����������֮��Ϊ9����4�ֱַ��ǣ�3��6������6��3����4��5����5��4����
���Թ˿͵õ�ϴ��ˮ�ĸ���=$\frac{4}{36}$=$\frac{1}{9}$��
��2������˵������ȷ�����������ӣ����ֳ��ϵĵ���֮�Ͳ�������1�Ľ������˳��в�������ƭ��Ϊ��
���� ���⿼�����б�������״ͼ���������б�������״ͼ��չʾ���п��ܵĽ�����n���ٴ���ѡ�������¼�A��B�Ľ����Ŀm��������ʣ�

��ϰ��ϵ�д�
�����Ŀ
20��Ϊ�μ�2016�ꡰ�����г��б�ҵ����ѧ�������ԡ���С��ͬѧ�̿�ѵ������������ϰ�У����5�������ijɼ�����λ����/���ӣ�Ϊ150��158��162��158��166���������ݵ���������λ�������ǣ�������
| A�� | 158��158 | B�� | 158��162 | C�� | 162��160 | D�� | 160��160 |
1���������������������������������
�ٶԽ�����ȵ��ı����Ǿ��Σ�
����������ֱ�ǵ��ı����Ǿ��Σ�
����һ������ֱ�ǵ�ƽ���ı����Ǿ��Σ�
�ٶԽ�����ȵ��ı����Ǿ��Σ�
����������ֱ�ǵ��ı����Ǿ��Σ�
����һ������ֱ�ǵ�ƽ���ı����Ǿ��Σ�
| A�� | 3�� | B�� | 2�� | C�� | 1�� | D�� | 0�� |
18���ݳ���ͳ�ƣ�2015�걱����ʵ�ֵ���������ֵ��GDP��ԼΪ1134.6��Ԫ������1134.6��Ԫ�ÿ�ѧ��������ʾΪ��������
| A�� | 1134.6��108Ԫ | B�� | 11.346��1010Ԫ | C�� | 1.1346��1011Ԫ | D�� | 1.1346��1012Ԫ |
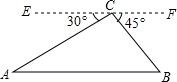 ��ͼ����������C����õ���A��B����ĸ��Ƿֱ�Ϊ30�㣬45�㣬��ʱ������C������λ�õ������ϵ�A�ľ���Ϊ400�ף��������A��B�����ľ��룮
��ͼ����������C����õ���A��B����ĸ��Ƿֱ�Ϊ30�㣬45�㣬��ʱ������C������λ�õ������ϵ�A�ľ���Ϊ400�ף��������A��B�����ľ��룮
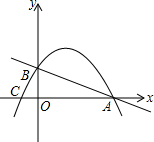 ��ͼ����ֱ֪��y=-$\frac{1}{2}$x+2��x�ᡢy��ֱ��ཻ��A��B���㣬��A��B�����������y=ax2+bx+c��x���ڵ�C��-1��0����
��ͼ����ֱ֪��y=-$\frac{1}{2}$x+2��x�ᡢy��ֱ��ཻ��A��B���㣬��A��B�����������y=ax2+bx+c��x���ڵ�C��-1��0����