题目内容
 如图,正方形ABCD的边长是4cm,点G在边AB上,以BG为边向外作正方形GBFE,连结AE、AC、CE,则△AEC的面积是
如图,正方形ABCD的边长是4cm,点G在边AB上,以BG为边向外作正方形GBFE,连结AE、AC、CE,则△AEC的面积是考点:正方形的性质
专题:
分析:把图形补全成矩形,设正方形GBFE的边长为x,求出矩形HFCD的面积等于4(x+4),再求出△EFC、△ACD、△AHE的面积分别为
x(x+4)、
×4×4、
x(4-x),△AEC的面积等于矩形HFCD的面积减去△EFC、△ACD、△AHE的面积,整理即可.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:如图,图形补全成矩形HFCD,设正方形GBFE的边长为x,则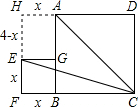
S矩形HFCD=4(x+4),S△EFC=
x(x+4)、S△ACD=
×4×4、S△AHE=
x(4-x),
∵△AEC的面积=S矩形HFCD-S△EFC-S△ACD-S△AHE
=4(x+4)-
x(x+4)-
×4×4-
x(4-x)
=4x+8-
x(x+4+4-x)
=8cm2.
故答案为:8.

S矩形HFCD=4(x+4),S△EFC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵△AEC的面积=S矩形HFCD-S△EFC-S△ACD-S△AHE
=4(x+4)-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=4x+8-
| 1 |
| 2 |
=8cm2.
故答案为:8.
点评:本题考查了正方形的性质和三角形的面积,补全图形是解题的关键,同学们容易在整式的运算中出错,计算时一定要仔细.

练习册系列答案
相关题目
在△ABC中,CA=CB,以△ABC的边BC向外侧作正方形BCDE,若记∠DAB的度数为α,则关于α的值下列说法正确的是( )
| A、视△ABC而定 |
| B、α<∠CAB |
| C、45°<α<90° |
| D、与△ABC形状无关 |
下列方程中,关于x的一元二次方程是( )
| A、(x+1)2=2(x+1) | ||||
B、
| ||||
| C、ax2+bx+c=0 | ||||
| D、x2+2x=x2-1 |
 如图,在△ABC中,∠B=60°,CE平分∠ACB,AD平分∠BAC,AD与CE交于F.
如图,在△ABC中,∠B=60°,CE平分∠ACB,AD平分∠BAC,AD与CE交于F.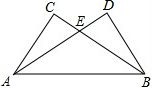 如图所示,CE=DE,EA=EB,CA=DB,求证:△ABC≌△BAD.
如图所示,CE=DE,EA=EB,CA=DB,求证:△ABC≌△BAD.