题目内容
20. 如图,在平行四边形ABCD中,过对角线AC与BD的交点O作AC的垂线交AD于点E,连接CE.若AB=4,BC=6,则△CDE的周长是( )
如图,在平行四边形ABCD中,过对角线AC与BD的交点O作AC的垂线交AD于点E,连接CE.若AB=4,BC=6,则△CDE的周长是( )| A. | 7 | B. | 10 | C. | 11 | D. | 12 |
分析 由平行四边形ABCD的对角线相交于点O,OE⊥AC,根据线段垂直平分线的性质,可得AE=CE,又由平行四边形ABCD的AB+BC=AD+CD=10,继而可得△CDE的周长等于AD+CD.
解答 解:∵四边形ABCD是平行四边形,
∴OA=OC,AB=CD,AD=BC,
∵AB=4,BC=6,
∴AD+CD=10,
∵OE⊥AC,
∴AE=CE,
∴△CDE的周长为:CD+CE+DE=CD+CE+AE=AD+CD=10.
故选B.
点评 此题考查了平行四边形的性质,关键是根据线段垂直平分线的性质进行分析.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
5.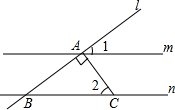 如图,m∥n,直线l分别交m,n于点A,点B,AC⊥AB,AC交直线n于点C,若∠1=35°,则∠2等于( )
如图,m∥n,直线l分别交m,n于点A,点B,AC⊥AB,AC交直线n于点C,若∠1=35°,则∠2等于( )
 如图,m∥n,直线l分别交m,n于点A,点B,AC⊥AB,AC交直线n于点C,若∠1=35°,则∠2等于( )
如图,m∥n,直线l分别交m,n于点A,点B,AC⊥AB,AC交直线n于点C,若∠1=35°,则∠2等于( )| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
6.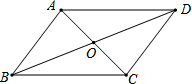 如图,?ABCD的对角线AC、BD相交于点O,则下列说法一定正确的是( )
如图,?ABCD的对角线AC、BD相交于点O,则下列说法一定正确的是( )
 如图,?ABCD的对角线AC、BD相交于点O,则下列说法一定正确的是( )
如图,?ABCD的对角线AC、BD相交于点O,则下列说法一定正确的是( )| A. | AO=OD | B. | AO⊥OD | C. | AO=OC | D. | AO⊥AB |
8.下列各数中,最小的数是( )
| A. | -0.5 | B. | 0 | C. | -2 | D. | 1 |
12.-$\frac{1}{2015}$的倒数为( )
| A. | -2015 | B. | -$\frac{1}{2015}$ | C. | 2015 | D. | $\frac{1}{2015}$ |
10. 图中几何体的主视图是( )
图中几何体的主视图是( )
 图中几何体的主视图是( )
图中几何体的主视图是( )| A. |  | B. |  | C. |  | D. |  |
