题目内容
已知:如图,在平面直角坐标系xOy中,一次函数y=-x的图象与反比例函数y=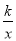 的图象交于A、B两点.
的图象交于A、B两点.
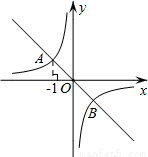
(1)求k的值;
(2)如果点P在y轴上,且满足以点A、B、P为顶点的三角形是直角三角形,直接写出点P的坐标.
(1)-1;(2)P点坐标为(0,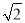 )、(0,-
)、(0,-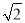 )、(0,2)、(0,-2).
)、(0,2)、(0,-2).
【解析】
试题分析:(1)首先求出A点坐标,再把A点坐标代入y=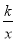 即可得到k的值;
即可得到k的值;
(2)BD⊥y轴,AC⊥y轴,如图,设P点坐标为(0,y),先根据对称得到B点坐标为(1,-1),再根据勾股定理得到AB2=22+22=8,PB2=PD2+BD2=(y+1)2+12,PA2=PC2+AC2=(y-1)2+12,然后分类讨论:当△APB是以AB为斜边的直角三角形,则PB2+PA2=AB2;当△APB是以PB为斜边的直角三角形,则AB2+PA2=PB2;当△APB是以PA为斜边的直角三角形,AB2+PB2=PA2,分别得到关于y的方程,解方程求出y的值即可得到P点坐标.
试题解析:(1)∵一次函数y=-x的图象与反比例函数y=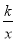 的图象交于A、B两点,
的图象交于A、B两点,
根据图象可得出A点横坐标为-1,代入一次函数解析式,
∴y=-(-1)=1,
∴A点坐标为:(-1,1),
∵反比例函数y=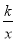 的图象经过点A(-1,1),
的图象经过点A(-1,1),
∴k=-1×1=-1;
(2)作BD⊥y轴,AC⊥y轴,如图,设P点坐标为(0,y),
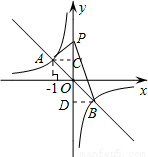
∵点A与B点关于原点对称,
∴B点坐标为(1,-1),
∴AB2=22+22=8,PB2=PD2+BD2=(y+1)2+12,PA2=PC2+AC2=(y-1)2+12,
分类:当△APB是以AB为斜边的直角三角形,则PB2+PA2=AB2,
∴PB2+PA2=AB2,即(y+1)2+12+(y-1)2+12=8,解得y=±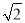 ;
;
当△APB是以PB为斜边的直角三角形,
∴AB2+PA2=PB2,即(y+1)2+12=(y-1)2+12+8,解得y=2;
当△APB是以PA为斜边的直角三角形,
∴AB2+PB2=PA2,即(y-1)2+12=(y+1)2+12+8,解得y=-2;
∴P点坐标为(0,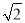 )、(0,-
)、(0,-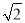 )、(0,2)、(0,-2).
)、(0,2)、(0,-2).
考点:反比例函数与一次函数的交点问题.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案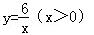 的图象交于A(m,6),B(3,n)两点.
的图象交于A(m,6),B(3,n)两点.
 的x的取值范围;
的x的取值范围; 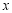 的一元二次方程
的一元二次方程 有两个不相等的实数根,则
有两个不相等的实数根,则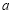 的取值范围是( )
的取值范围是( )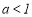 B.
B.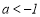 C.
C.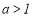 D.
D.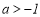


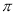 D.16
D.16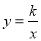 的图象经过点C,则k的值为 .
的图象经过点C,则k的值为 .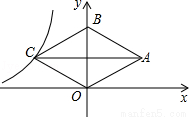

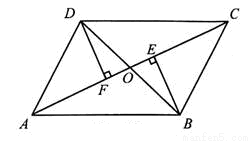
 BD,则四边形ABCD是什么特殊四边形?请说明理由.
BD,则四边形ABCD是什么特殊四边形?请说明理由.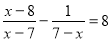 ,可知方程( ).
,可知方程( ).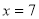 B.解为
B.解为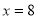 C.解为
C.解为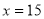 D.无解
D.无解