题目内容
等腰三角形一边是5,腰上的高是3,则这个等腰三角形的周长是 .
考点:勾股定理,等腰三角形的性质
专题:分类讨论
分析:作出图形,分①5是腰长时,利用勾股定理列式求出AD,再分CD在三角形内部和外部两种情况求出BD,利用勾股定理列式求出BC,然后根据三角形的周长的定义解答;②5是底边时,利用勾股定理列式求出BD,过点A作AE⊥BC于E,根据等腰三角形三线合一的性质求出BE,然后利用∠B的余弦列式求出腰长,再根据三角形的周长的定义解答.
解答: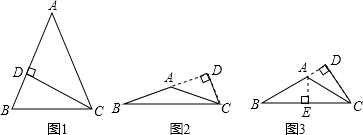 解:①5是腰长时,由勾股定理得,AD=
解:①5是腰长时,由勾股定理得,AD=
=4,
如图1,高CD在三角形内部时,BD=AB-AD=5-4=1,
在Rt△BCD中,BC=
=
,
三角形的周长=5+5+
=10+
;
如图2,高CD在三角形外部时,BD=AB+AD=5+4=9,
在Rt△BCD中,BC=
=3
,
三角形的周长=5+5+3
=10+3
;
②如图3,5底边时,由勾股定理得,BD=
=4,
过点A作AE⊥BC于E,则BE=
BC=
,
∵cos∠B=
=
,
∴
=
,
解得AB=
,
三角形的周长=
×2+5=
.
综上所述,三角形的周长为10+
或10+3
或
.
故答案为:10+
或10+3
或
.
 解:①5是腰长时,由勾股定理得,AD=
解:①5是腰长时,由勾股定理得,AD=| 52-32 |
如图1,高CD在三角形内部时,BD=AB-AD=5-4=1,
在Rt△BCD中,BC=
| 32+12 |
| 10 |
三角形的周长=5+5+
| 10 |
| 10 |
如图2,高CD在三角形外部时,BD=AB+AD=5+4=9,
在Rt△BCD中,BC=
| 32+92 |
| 10 |
三角形的周长=5+5+3
| 10 |
| 10 |
②如图3,5底边时,由勾股定理得,BD=
| 52-32 |
过点A作AE⊥BC于E,则BE=
| 1 |
| 2 |
| 5 |
| 2 |
∵cos∠B=
| BE |
| AB |
| BD |
| BC |
∴
| ||
| AB |
| 4 |
| 5 |
解得AB=
| 25 |
| 8 |
三角形的周长=
| 25 |
| 8 |
| 45 |
| 4 |
综上所述,三角形的周长为10+
| 10 |
| 10 |
| 45 |
| 4 |
故答案为:10+
| 10 |
| 10 |
| 45 |
| 4 |
点评:本题考查了勾股定理,等腰三角形的性质,锐角三角函数,难点在于分情况讨论,作出图形更形象直观.

练习册系列答案
相关题目
 某商场举行店庆酬宾促销活动,商场规定:顾客每购买99元的商品,就能获得一次抽奖的机会,如果顾客不愿意抽奖,可以直接获得购物券10元.商场内设立了多个抽奖点,为了吸引顾客商场电子屏实时显示抽奖状况,下面是一位顾客用手机拍下的电子屏画面:
某商场举行店庆酬宾促销活动,商场规定:顾客每购买99元的商品,就能获得一次抽奖的机会,如果顾客不愿意抽奖,可以直接获得购物券10元.商场内设立了多个抽奖点,为了吸引顾客商场电子屏实时显示抽奖状况,下面是一位顾客用手机拍下的电子屏画面: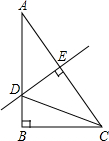 如图,在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD,若BD=1,则AD的长是( )
如图,在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD,若BD=1,则AD的长是( )