题目内容
13.已知:abc≠0,则$\frac{a}{5|a|}+\frac{|b|}{5b}+\frac{c}{5|c|}+\frac{abc}{{5|{abc}|}}$=-$\frac{4}{5}$或0或$\frac{4}{5}$.分析 根据a、b、c中负因数的个数进行分类计算即可.
解答 解:当a、b、c均为正数时,原式=$\frac{1}{5}$+$\frac{1}{5}$+$\frac{1}{5}$+$\frac{1}{5}$=$\frac{4}{5}$,
当a、b、c中有一个负数时,原式=0;
当a、b、c中有两个负数时,原式=0,
当a、b、c均为负数时,原式=-$\frac{4}{5}$.
故答案为:-$\frac{4}{5}$或0或$\frac{4}{5}$.
点评 本题主要考查的是绝对值的性质,分类讨论是解题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
3.随着计算机技术的发展,电脑价格不断降低,某品牌的电脑按原价降低m元之后又降20%,现售价为n元,那么该电脑的原售价为( )
| A. | ($\frac{4}{5}$n+m)元 | B. | ($\frac{5}{4}$n+m)元 | C. | (5m+n) 元 | D. | (5n+m)元 |
1.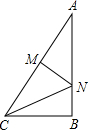 如图,在Rt△ABC中,∠B=90°,AC=10,BC=6,线段AC的垂直平分线MN分别交AC、AB于M、N两点,则CN的长为( )
如图,在Rt△ABC中,∠B=90°,AC=10,BC=6,线段AC的垂直平分线MN分别交AC、AB于M、N两点,则CN的长为( )
 如图,在Rt△ABC中,∠B=90°,AC=10,BC=6,线段AC的垂直平分线MN分别交AC、AB于M、N两点,则CN的长为( )
如图,在Rt△ABC中,∠B=90°,AC=10,BC=6,线段AC的垂直平分线MN分别交AC、AB于M、N两点,则CN的长为( )| A. | $\frac{35}{8}$ | B. | $\frac{25}{4}$ | C. | $\frac{25}{2}$ | D. | 7 |
2.下列事件中,必然事件的是( )
| A. | a是实数,-a2≤0 | |
| B. | 天上打雷后就下雨 | |
| C. | 掷一枚质地均匀的硬币一次,反面朝上 | |
| D. | 某运动员跳高的最好成绩是200.1米 |
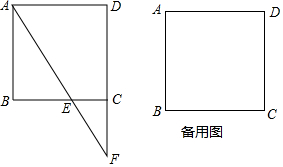 已知边长为3的正方形ABCD中,点E在射线BC上,且BE=2CE,连结AE交射线DC于点F,将△ABE沿直线AE翻折,点B落在点B1处.
已知边长为3的正方形ABCD中,点E在射线BC上,且BE=2CE,连结AE交射线DC于点F,将△ABE沿直线AE翻折,点B落在点B1处.