题目内容
13.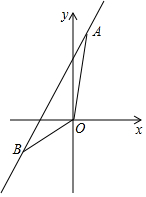 如图,直线l经过点A(1,6)和点B(-3,-2).
如图,直线l经过点A(1,6)和点B(-3,-2).(1)求直线l的解析式,直线与坐标轴的交点坐标;
(2)求△AOB的面积.
分析 (1)利用待定系数法求出直线l的解析式,解一元一次方程求出直线与坐标轴的交点坐标;
(2)结合图形、根据三角形的面积公式计算即可.
解答 解:(1)设直线解析式为y=kx+b,
把点A(1,6)和点B(-3,-2)代入,
得,$\left\{\begin{array}{l}{k+b=6}\\{-3k+b=-2}\end{array}\right.$,
解得:k=2,b=4,
所以,y=2x+4,
x=0时,y=4,
y=0时,x=-2,
则直线与x轴交点为(-2,0),与y轴交点为(0,4),
(2)△AOB的面积$\frac{1}{2}×$2×6$+\frac{1}{2}×$2×2=8.
点评 本题考查的是一次函数解析式的求法,灵活运用待定系数法求一次函数解析式是解题的关键.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
4.如果关于x的方程x2-2x-k=0有两个相等的实数根,那么以下结论正确的是( )
| A. | k=-1 | B. | k=1 | C. | k>-1 | D. | k>1 |
1.随着互联网进入成熟发展阶段,手机已成为我们生活中必不可少的信息交流工具,某商场计划购进A、B两种不同品牌的手机共50部,A、B两种品牌的手机的进价和售价如表所示:
设该商场计划购进A品牌手机x台,两种品牌的手机全部销售完后可获得利润为y元.
(1)求y与x之间的函数关系式;
(2)若商场购进B品牌手机的数量为20部,两种品牌的手机全部销售完后可获利多少?
| 品牌 价格 | A品牌 | B品牌 |
| 进价(元/部) | 3800 | 3000 |
| 售价(元/部) | 4500 | 3500 |
(1)求y与x之间的函数关系式;
(2)若商场购进B品牌手机的数量为20部,两种品牌的手机全部销售完后可获利多少?
8.已知反比例函数y=$\frac{3}{x}$,在此函数图象上的点是( )
| A. | (-1,1) | B. | (1,1) | C. | (1,3) | D. | (-1,3) |
18.下列各式属于最简二次根式的是( )
| A. | $\sqrt{0.2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{\frac{1}{2}}$ | D. | $\sqrt{12}$ |
5. 如图,已知直线a∥b,∠1=50°,则∠2的度数为( )
如图,已知直线a∥b,∠1=50°,则∠2的度数为( )
 如图,已知直线a∥b,∠1=50°,则∠2的度数为( )
如图,已知直线a∥b,∠1=50°,则∠2的度数为( )| A. | 40° | B. | 50° | C. | 130° | D. | 150° |
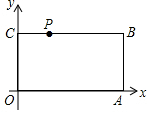 如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A,C的坐标分别为A(10,0),C(0,4),点D是OA中点,点P在边BC上运动,当△ODP是等腰三角形时,点P的坐标为(2,4)或(2.5,4)或(3,4)或(8,4).
如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A,C的坐标分别为A(10,0),C(0,4),点D是OA中点,点P在边BC上运动,当△ODP是等腰三角形时,点P的坐标为(2,4)或(2.5,4)或(3,4)或(8,4).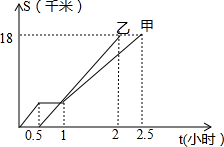 甲、乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离 S(千米)和行驶时间t(小时)之间的关系图象如图2所示,根据图中提供的信息,有下列说法:
甲、乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离 S(千米)和行驶时间t(小时)之间的关系图象如图2所示,根据图中提供的信息,有下列说法: