题目内容
过△ABC内一点P,作DE∥BC分别交AB、AC于D、E,作GF∥AC分别交AB、BC于G、F,作HK∥AB分别交BC、AC于H、K,则 的值是
的值是
- A.

- B.2
- C.

- D.

B
分析:根据已知推出平行四边形AGPK、BDPH,得出PK=AG,PH=BD,根据平行线分线段成比例定理得出 =
= ,
,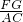 =
= ,代入即可求出答案.
,代入即可求出答案.
解答: 解:∵GF∥AC,HK∥AB,
解:∵GF∥AC,HK∥AB,
∴四边形AGPK是平行四边形,
∴PK=AG,
同理PH=BD,
∵DE∥BC,FG∥AC,
∴由平行线分线段成比例定理得: =
= ,
,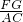 =
= ,
,
∴ +
+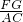 +
+ =
= +
+ +
+
=
=
=2.
故选B.
点评:本题主要考查对平行线分线段成比例定理,平行四边形的性质和判定等知识点的理解和掌握,能熟练地根据平行线分线段成比例定理进行推理是解此题的关键.
分析:根据已知推出平行四边形AGPK、BDPH,得出PK=AG,PH=BD,根据平行线分线段成比例定理得出
 =
= ,
,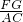 =
= ,代入即可求出答案.
,代入即可求出答案.解答:
 解:∵GF∥AC,HK∥AB,
解:∵GF∥AC,HK∥AB,∴四边形AGPK是平行四边形,
∴PK=AG,
同理PH=BD,
∵DE∥BC,FG∥AC,
∴由平行线分线段成比例定理得:
 =
= ,
,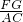 =
= ,
,∴
 +
+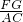 +
+ =
= +
+ +
+
=

=

=2.
故选B.
点评:本题主要考查对平行线分线段成比例定理,平行四边形的性质和判定等知识点的理解和掌握,能熟练地根据平行线分线段成比例定理进行推理是解此题的关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
 如图,过△ABC内一点M做各边的平行线与各边分别交于D,E,F,G,L,N各点.求证:
如图,过△ABC内一点M做各边的平行线与各边分别交于D,E,F,G,L,N各点.求证: 如图,过△ABC内一点分别作三边的平行线,形成三个小三角形①、②、③,如果这三个小三角形面积分别为1、4、9,则△ABC的面积为
如图,过△ABC内一点分别作三边的平行线,形成三个小三角形①、②、③,如果这三个小三角形面积分别为1、4、9,则△ABC的面积为 如图,过△ABC内一点M做各边的平行线与各边分别交于D,E,F,G,L,N各点.求证:
如图,过△ABC内一点M做各边的平行线与各边分别交于D,E,F,G,L,N各点.求证: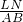 =2.
=2. +
+ +
+ =2.
=2.