题目内容
8.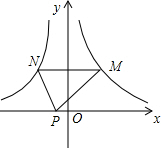 如图,点M是反比例函数y=$\frac{5}{x}$(x>0)图象上的一个动点,过点M作x轴的平行线交反比例函数y=-$\frac{5}{x}$(x<0)图象于点N.
如图,点M是反比例函数y=$\frac{5}{x}$(x>0)图象上的一个动点,过点M作x轴的平行线交反比例函数y=-$\frac{5}{x}$(x<0)图象于点N.(1)函数y=$\frac{5}{x}$(x>0)与y=-$\frac{5}{x}$(x<0)关于y轴对称;
(2)若点M($\frac{5}{3}$,3),求点N的坐标;
(3)若点P是x轴上的任意一点,那么△PMN的面积是否发生变化?若不变,求出它的面积是多少?若变化,请说明理由.
分析 (1)直接根据函数图象即可得出结论;
(2)根据两函数的图象关于y轴对称的特点可直接得出结论;
(3)根据同底等高的三角形面积相等可知△PMN的面积不变,再由三角形的面积公式可得出结论.
解答 解:(1)由函数图象可知,函数y=$\frac{5}{x}$(x>0)与y=-$\frac{5}{x}$(x<0)关于y轴对称.
故答案为:y;
(2)∵两函数图象关于y轴对称,
∴点M、N关于y轴对称,
∴N(-$\frac{5}{3}$,3);
(3)不变.
∵M($\frac{5}{3}$,3),N(-$\frac{5}{3}$,3),
∴MN=2×$\frac{5}{3}$=$\frac{10}{3}$,
∴S△PMN=$\frac{1}{2}$×$\frac{10}{3}$×3=5.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
3.下列命题中正确的是( )
| A. | 圆是轴对称图形,任何一条直径都是它的对称轴 | |
| B. | 平分弦的直径垂直于弦,并且平分弦所对的弧 | |
| C. | 相等的圆心角所对的弧相等,所对的弦相等 | |
| D. | 在同圆或等圆中,同弧或等弧所对的圆心角相等 |


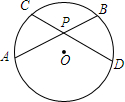 如图,已知⊙O的弦AB,CD相交于点P,PO平分∠APD,求证:AB=CD.
如图,已知⊙O的弦AB,CD相交于点P,PO平分∠APD,求证:AB=CD.