题目内容
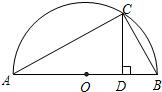
如图，AB为半圆O的直径，C是半圆上一点，且∠COA=60°，设扇形AOC、△COB、弓形BmC的面积为S1、S2、S3，则它们之间的关系是
- A.S1＜S2＜S3
- B.S2＜S1＜S3
- C.S1＜S3＜S2
- D.S3＜S2＜S1
B
分析：设出半径，作出△COB底边BC上的高，利用扇形的面积公式和三角形的面积公式表示出三个图形面积，比较即可求解．
解答：
解：作OD⊥BC交BC与点D，则∠COD=60°．
∴S扇形AOC=
；
S扇形BOC=
．
在三角形OCD中，∠OCD=30°，
∴OD=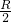
，CD=
，BC=
R，
∴S△OBC=
，S弓形=
=
，
＞
＞，∴S2＜S1＜S3
故选B．
点评：此题考查扇形面积公式及弓形面积公式，解题的关键是算出三个图形的面积，首先利用扇形公式计算出第一个扇形的面积，再利用弓形等于扇形-三角形的关系求出弓形的面积，进行比较得出它们的面积关系．
分析：设出半径，作出△COB底边BC上的高，利用扇形的面积公式和三角形的面积公式表示出三个图形面积，比较即可求解．
解答：
解：作OD⊥BC交BC与点D，则∠COD=60°．∴S扇形AOC=
；S扇形BOC=
．在三角形OCD中，∠OCD=30°，
∴OD=
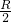，CD=，BC=R，∴S△OBC=
，S弓形==，＞＞，∴S2＜S1＜S3故选B．
点评：此题考查扇形面积公式及弓形面积公式，解题的关键是算出三个图形的面积，首先利用扇形公式计算出第一个扇形的面积，再利用弓形等于扇形-三角形的关系求出弓形的面积，进行比较得出它们的面积关系．
练习册系列答案
相关题目
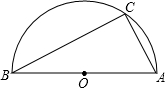
为D，AD=a，DB=b．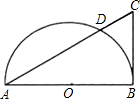
如图，AB为半圆O的直径，CB切半圆于点B，AC交半圆于点D，若CD=1，AD=3，则⊙O半径的长为
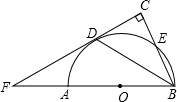C，直线CD交BA的延长线于点F．
如图，AB为半圆O的直径，B1，B2，…，Bk是半圆上的k个点，满足BB1=B1B2=…Bk-1Bk，对于线段OB1，OB2，…，OBk，AB1，AB2，…，ABk，当k=4时，有