题目内容
【题目】将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,
,![]() 的延长线与
的延长线与![]() 相交于点
相交于点![]() ,连接
,连接![]() 、
、![]() .
.
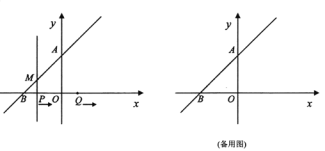
![]() 如图
如图![]() ,若
,若![]() ,
,![]() .
.
①求证:![]() ;②猜想线段
;②猜想线段![]() 、
、![]() 的数量关系,并证明你的猜想;
的数量关系,并证明你的猜想;
![]() 如图
如图![]() ,若
,若![]() ,
,![]() (
(![]() 为常数),求
为常数),求![]() 的值(用含
的值(用含![]() 、
、![]() 的式子表示).
的式子表示).

【答案】![]() 证明①见解析; ②猜想:
证明①见解析; ②猜想:![]() ,证明见解析;
,证明见解析;![]()
![]() .
.
【解析】
(1)由旋转性质证明△ABD为等边三角形,则∠DAB=∠ABC=60°,所以DA∥BC;
(2)①如答图1所示,作辅助线(在DF上截取DG=AF,连接BG),构造全等三角形△DBG≌△ABF,得到BG=BF,∠DBG=∠ABF;进而证明△BGF为等边三角形,则GF=BF=AF;从而DF=2AF;
②与①类似,作辅助线,构造全等三角形△DBG≌△ABF,得到BG=BF,∠DBG=∠ABF,由此可知△BGF为顶角为α的等腰三角形,解直角三角形求出GF的长度,从而得到DF长度,问题得解.
![]() 证明:①由旋转性质可知,
证明:①由旋转性质可知,![]() ,
,![]()
∴![]() 为等边三角形,
为等边三角形,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
②猜想:![]() .
.
证明:如答图![]() 所示,在
所示,在![]() 上截取
上截取![]() ,连接
,连接![]() .
.

由旋转性质可知,![]() ,
,![]() .
.
∵在![]() 与
与![]() 中,
中,

∴![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
又∵![]() ,
,
∴![]() 为等边三角形,
为等边三角形,
∴![]() ,又
,又![]() ,
,
∴![]() .
.
∴![]() .
.
![]() 解:如答图
解:如答图![]() 所示,在
所示,在![]() 上截取
上截取![]() ,连接
,连接![]() .
.

由![]() ,同理可证明
,同理可证明![]() ,
,![]() ,
,![]() .
.
过点![]() 作
作![]() 于点
于点![]() ,
,
∵![]() ,∴点
,∴点![]() 为
为![]() 中点,
中点,![]() .
.
在![]() 中,
中,![]() .
.
∴![]()
∴![]() ,
,
∴![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目