题目内容
在一边靠墙的空地上,用砖墙围成三格的矩形场地,已知砖墙在地面上占地总长度160m,分隔墙在地面上的长度为 时,所围场地总面积最大.
考点:二次函数的应用
专题:
分析:设矩形的面积为S,由矩形的面积公式可以得出S与x的关系,由关系式的性质就可以得出结论.
解答:解: 设矩形的面积为S,所围矩形ABCD的长AB为x米,由题意,得
设矩形的面积为S,所围矩形ABCD的长AB为x米,由题意,得
S=x•
(160-x)=-
(x-80)2+3200,
故当x=80时,S最大=3200,且符合题意.
则当所围矩形的长为80m、宽为40m时,能使矩形的面积最大,最大面积为3200 m2,
分隔墙在地面上的长度为80m,40m,40m时,所围场地总面积最大.
故答案为:80m,40m,40m.
 设矩形的面积为S,所围矩形ABCD的长AB为x米,由题意,得
设矩形的面积为S,所围矩形ABCD的长AB为x米,由题意,得S=x•
| 1 |
| 2 |
| 1 |
| 2 |
故当x=80时,S最大=3200,且符合题意.
则当所围矩形的长为80m、宽为40m时,能使矩形的面积最大,最大面积为3200 m2,
分隔墙在地面上的长度为80m,40m,40m时,所围场地总面积最大.
故答案为:80m,40m,40m.
点评:本题考查了二次函数的应用,解答时求出函数的解析式是关键.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
 如图,AB∥CD,AD∥BC;则图中的全等三角形共有( )
如图,AB∥CD,AD∥BC;则图中的全等三角形共有( )| A、5对 | B、4对 | C、3对 | D、2对 |
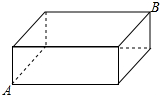 如图,是一个长9m,宽7m,高5m的仓库,在其内壁的A处有一只壁虎,B处有一只蚊子,则壁虎爬到蚊子处的最短距离为( )m.
如图,是一个长9m,宽7m,高5m的仓库,在其内壁的A处有一只壁虎,B处有一只蚊子,则壁虎爬到蚊子处的最短距离为( )m.| A、21m | B、15m |
| C、12m | D、13m |
下列说法中,正确的是( )
| A、两个互补的角中必有一个是钝角 |
| B、一个角的补角一定比这个角大 |
| C、互补的两个角中,至少有一个角大于或等于直角 |
| D、相等的角是对顶角 |