题目内容

精英家教网如图，以△ABC的一边AB为直径的圆交AC边于D，交BC边于E，连接DE，BD与AE交于点F．则sin∠CAE的值为（　　）
A、
DF
AD
B、
CD
AC
C、
EF
AF
D、
DE
AB
分析：根据题意，易得sin∠CAE=
CE
AC
，再由圆内接四边形的性质，易得∠CED=∠CAB，∠CDE=∠CBA，进而可得△CDE∽△CBA，由相似三角形的性质，可得
CE
AC
=
DE
AB
，进而可得答案．
解答：解：根据圆周角定理，易得∠AEB=90°，进而可得∠AEC=90°．
在Rt△AEC中，由锐角三角函数的定义，可得sin∠CAE=
CE
AC
．
由圆内接四边形的性质，可得∠CED=∠CAB，∠CDE=∠CBA，
可得△CDE∽△CBA，
则有
CE
AC
=
DE
AB
，
故有sin∠CAE=
DE
AB
．
故选D．
点评：本题考查锐角三角函数的定义，注意结合图形，找到直角三角形，进而由锐角三角函数的定义解题．
练习册系列答案
相关题目
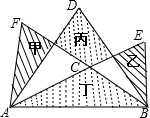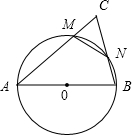精英家教网如图，以△ABC的边AB为直径画圆，与边AC交于M，与边BC交于N，已知△ABC的面积是△CMN面积的4倍，△ABC中有一个内角度数是另一内角度数的2倍，试计算△ABC三个内角的度数：
 
．
14、已知：如图分别以△ABC的每一条边，在三角形外作等边三角形，△ABD、△BCE、△ACF，则CD=AE=BF．（
√
）
精英家教网如图，以△ABC的每一条边为边作三个正三角形△ABD、△BCE和△ACF．已知这三个正三角形构成的图形中，甲、乙阴影部分的面积和等于丙、丁阴影部分的面积和，则∠FCE=（　　）
A、130°B、140°C、150°D、160°
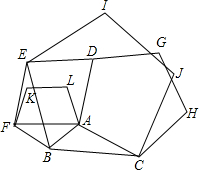（2012•拱墅区一模）如图，以△ABC的各边为边，在BC的同侧分别作三个正五边形．它们分别是正五边形ABFKL、BCJIE、ACHGD，试探究：
（1）四边形ADEF是什么四边形？
（2）当△ABC满足什么条件时，四边形ADEF是正方形？（不需证明）
（3）四边形ADEF一定存在吗？为什么？
如图，以△ABC的任意两边为平行四边形的一组邻边，第三边为平行四边形的一条对角线，作出所有的平行四边形．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网