Question

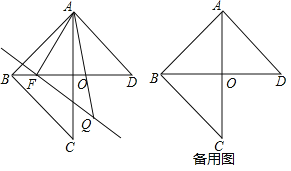
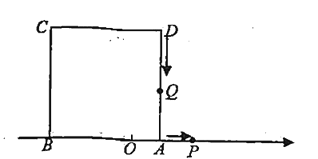
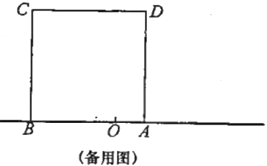
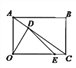
【题目】如图，在矩形ABCO中，AO=3， OC=4，设D、E分别是线段AC、OC上的动点，它们同时出发，点D以每秒3个单位的速度从点A向点C运动，点E以每秒1个单位的速度从点C向点O运动（不包含A、C两个端点）．当t=___________时，△ODE为直角三角形．

Answer 1

【答案】或1

【解析】

可分二种情况（①，∠ODE=90°，②∠DEO=90°）讨论，然后只需运用相似三角形的性质就可解决问题．

过点D作DH⊥OC于点H，如图1，

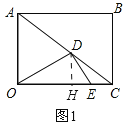
由题可知：AD=3t，CE=t，

∵OC=4，∴OE=OC-EC=4-t，

在Rt△AOC中，

∵∠AOC=90°，OA=3，OC=4，

∴AC==5．

∵∠DHC=∠AOC=90°，∠HCD=∠OCA，

∴△HCD∽△OCA，

∴，

∴，

∴DH=，CH=，

∴OH=OC-CH=4-=，

①若∠ODE=90°，如图1．

∵DH⊥OC，

∴∠DHO=∠DHE=90°，

∴∠ODH=90°-∠HDE=∠HED，

∴△DHO∽△EHD，

∴，

∴DH2=OHEH，

∴（）2=（-t），

整理得：19t2-34t+15=0，

解得：t1=1，t2=．

②若∠DEO=90°，如图2，

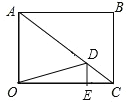
则∠DEC=∠AOC=90°，

∵∠ECD=∠OCA，

∴△DEC∽△AOC，

∴，

∴，

解得：t=．

综上所述：当以O、D、E三点为顶点的三角形是直角三角形时，t的值为1、、．