题目内容
如图，在△ABC中，∠B=90°，∠ACB=30°，∠BAD=75°，若BC=3，则CD=（ ）| A、3 | ||
| B、6 | ||
C、
| ||
D、2
|
考点：含30度角的直角三角形,等腰三角形的判定与性质,勾股定理
专题：
分析：根据∠B=90°，∠ACB=30°，得AC=2AB，再由BC=3，根据勾股定理得出AB和AC，又因为∠BAD=75°，则∠CAD=15°，所以∠ADC=15°，从而得出CD=AC．
解答：解：∵∠B=90°，∠ACB=30°，
∴AC=2AB，
设AB=x，则AC=2x，
∵BC=3，
∴x2+9=4x2，
∴x=
，
∵∠BAD=75°，
∴∠CAD=15°，
∴∠ADC=15°，
∴CD=AC．
∴CD=2
，
故选D．
∴AC=2AB，
设AB=x，则AC=2x，
∵BC=3，
∴x2+9=4x2，
∴x=
| 3 |
∵∠BAD=75°，
∴∠CAD=15°，
∴∠ADC=15°，
∴CD=AC．
∴CD=2
| 3 |
故选D．
点评：本题考查了含30度角的直角三角形、等腰三角形的判定以及勾股定理，所运用的知识点有：等腰三角形的性质、直角三角形的性质以及三角形外角的性质．
练习册系列答案
相关题目
”的字样，则它T恤上的数字实际是一个宾馆有二人间、三人间、四人间三种客房供游客租住，某旅行团25人准备同时租用这三种客房共9间，如果每个房间都住满，则租房方案共有（ ）
| A、4种 | B、3种 | C、2种 | D、1种 |
在下列各数中是无理数的有（ ）
-0.333…，
，
，-π，
，3.1415，2.010101．
-0.333…，
| 2 |
| 4 |
| 22 |
| 7 |
| A、2个 | B、4个 | C、5个 | D、6个 |
某停车场的收费标准如下：中型汽车的停车费为6元/辆，小型汽车的停车费为4元/辆．现在停车场中共有中、小型汽车50辆，这些车共缴纳停车费230元．四名同学都设未知数x，y，并根据题意，分别列出以下四个方程组，其中不正确的是（ ）
A、
| |||||||||
B、
| |||||||||
C、
| |||||||||
D、
|
下列事件中，必然事件是（ ）
| A、抛掷一枚硬币，正面朝上 |
| B、打开电视，正在播放广告 |
| C、体育课上，小刚跑完1000米所用时间为1分钟 |
| D、袋中只有4个球，且都是红球，任意摸出一球是红球 |
如图，图①、图②、图③分别表示甲、乙、丙三人由A地到B地的路线图（箭头表示行进方向）其中图②中E为AB的中点，图③中AH＞BH，我们用a、b、c分别代表三人走过的路程，则a、b、c的大小关系为（ ）
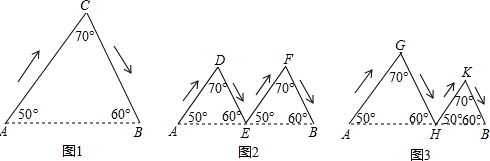
| A、a＞b=c |
| B、a＜b=c |
| C、a＞b＞c |
| D、a=b=c |