题目内容
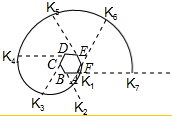如图，六边形ABCDEF是正六边形， |
| FK1 |
|
| K1K2 |
|
| K2K3 |
|
| K3K4 |
|
| K4K5 |
|
| K5K6 |
考点：弧长的计算
专题：规律型
分析：利用弧长公式，分别计算出l1，l2，l3，…的长，寻找其中的规律，确定l2013的长．
解答：解：根据题意得：l1=
=
，
l2=
=
，
l3=
=
=π，
l4=
=
，
按照这种规律可以得到：ln=
，
所以l2013=
=671π．
故答案为671π．
| 60π×1 |
| 180 |
| π |
| 3 |
l2=
| 60π×2 |
| 180 |
| 2π |
| 3 |
l3=
| 60π×3 |
| 180 |
| 3π |
| 3 |
l4=
| 60π×4 |
| 180 |
| 4π |
| 3 |
按照这种规律可以得到：ln=
| nπ |
| 3 |
所以l2013=
| 2013π |
| 3 |
故答案为671π．
点评：本题考查的是弧长的计算，先用公式计算，找出规律，求出l2013的长．
练习册系列答案
相关题目
如图，在Rt△ABC中，∠ABC=90°，BA=BC，D为AB的中点，连接CD，过点B作BG⊥CD，分别交CD、CA于点E、F，与过点A且垂直于AB的直线相交于点G，连结DF．
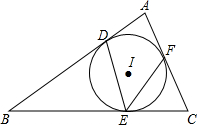如图，⊙I是△ABC的内切圆，与AB、BC、CA分别相切于点D、E、F，∠DEF=50°，求∠A的度数为（ ）| A、50° | B、80° |
| C、100° | D、60° |
下列多项式中是二次二项式的是（ ）
| A、3x2+2x+1 |
| B、-x4+9 |
| C、x2-2x |
| D、x3-3x2+4 |
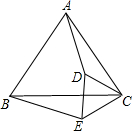如图所示，已知：△ABC和△CDE都是等边三角形，求证：AD=BE．
如图所示，已知O是直线AB上的一点，∠1=40°，OD平分∠BOC，则∠2=