题目内容
某工厂生产的某种产品按质量分为10个档次.第1档次(最低档次)的产品一天能生产76件,每件利润10元.每提高一个档次,每件利润增加2元,但一天产量减少4件.
(1)若生产第x档次的产品一天的总利润为y元(其中x为正整数,且1≤x≤10),求出y关于x的函数关系式;
(2)若生产第x档次的产品一天的总利润为1080元,求该产品的质量档次.
(1)y=-8x2+128x+640.(2)在第5档次时,一天的总利润为1080元.
【解析】
试题分析:(1)每件的利润为10+2(x-1),生产件数为76-4(x-1),则y=[10+2(x-1)][76-4(x-1)];
(2)由题意可令y=1080,求出x的实际值即可.
试题解析:(1)据题意可得y=[10+2(x-1)][76-4(x-1)]
整理,得y=-8x2+128x+640.
(2)当利润是1080元时,即-8x2+128x+640=1080
解得x1=5,x2=11,
因为x=11>10,不符合题意,舍去.
因此取x=5,
当生产产品的质量档次是在第5档次时,一天的总利润为1080元.
考点:二次函数的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 与
与 轴只有一个交点,且过点
轴只有一个交点,且过点 ,
, ,则
,则 ______.
______. 轴的正半轴上,连结CE、AD、
轴的正半轴上,连结CE、AD、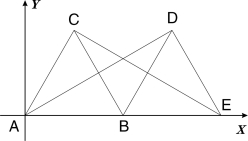
 的图象经过点(5,﹣1).则实数k的值是
的图象经过点(5,﹣1).则实数k的值是  时,原方程应变形为( )
时,原方程应变形为( ) B、
B、 C、
C、 D、
D、
 是二次函数,则m=______.
是二次函数,则m=______.

 B.
B. C.
C. D.2
D.2