题目内容
3、如图所示.AE∥BD,∠1=3∠2,∠2=25°,求∠C.

分析:利用平行线的性质,可以将角“转移”到新的位置,如∠1=∠DFC或∠AFB.若能将∠1,∠2,∠C“集中”到一个顶点处,则有∠1=∠DFC=∠C+∠2,即∠C=∠1-∠2=2∠2=50°.
解答:
解:过F到FG∥CB,交AB于G
∴∠C=∠AFG(同位角相等)
∴∠2=∠BFG(内错角相等)
∵AE∥BD
∴∠1=∠BFA(内错角相等)
∴∠C=∠AFG=∠BFA-∠BFG
=∠1-∠2=3∠2-∠2
=2∠2=50°.
故答案为50°.

解:过F到FG∥CB,交AB于G
∴∠C=∠AFG(同位角相等)
∴∠2=∠BFG(内错角相等)
∵AE∥BD
∴∠1=∠BFA(内错角相等)
∴∠C=∠AFG=∠BFA-∠BFG
=∠1-∠2=3∠2-∠2
=2∠2=50°.
故答案为50°.
点评:本题考查平行线的性质.运用平行线的性质,将角集中到适当位置,是添加辅助线(平行线)的常用技巧.角的等量代换的运用是正确解答本题的关键.

练习册系列答案
相关题目
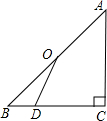 已知:如图,点O是等腰直角△ABC斜边AB的中点,D为BC边上任意一点.
已知:如图,点O是等腰直角△ABC斜边AB的中点,D为BC边上任意一点. 3、如图所示,AE、BD相交于点C,要使△ABC≌△EDC,至少要添加的条件是
3、如图所示,AE、BD相交于点C,要使△ABC≌△EDC,至少要添加的条件是 如图所示,AE是△FCD的中位线,BD∥AC,A,E,B三点共线,AB=8,FA=FE=6,则下列说法:①BE=4;②∠DEB=∠DBE;③AF=BD;④CD=2AE.正确的结论是( )
如图所示,AE是△FCD的中位线,BD∥AC,A,E,B三点共线,AB=8,FA=FE=6,则下列说法:①BE=4;②∠DEB=∠DBE;③AF=BD;④CD=2AE.正确的结论是( )