题目内容
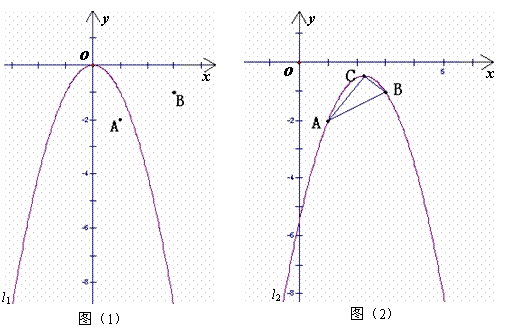
如图（1），在平面直角坐标系中，点A的坐标为（1，-2），点B的坐标为（3，-1），二次函数
的图象为
.
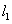（1）平移抛物线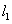，使平移后的抛物线过点A，但不过点B，写出平移后的抛物线的一个解析式（任写一个即可）.
（2）平移抛物线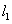，使平移后的抛物线过A、B两点，记抛物线为
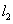，如图（2），求抛物线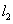的函数解析式及顶点C的坐标.
（3）设P为y轴上一点，且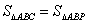
，求点P的坐标.
（4）请在图（2）上用尺规作图的方式探究抛物线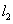上是否存在点Q，使
为等腰三角形. 若存在，请判断点Q共有几个可能的位置（保留作图痕迹）；若不存在，请说明理由.
（1）
等 （满足条件即可）
（2）设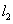的解析式为
，联立方程组
，
解得：
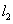，则的解析式为
，
点C的坐标为（
）
（3）如答图25-1，过点A、B、C三点分别作x轴的垂线，垂足分别为D、E、F，则
，
，
，
，
，
.
得：
.
延长BA交y轴于点G，直线AB的解析式为
，则点G的坐标为（0，
），设点P的坐标为（0，
）
①当点P位于点G的下方时，
，连结AP、BP，则
，又
，得
，点P的坐标为（0，
）.
②当点P位于点G的上方时，
，同理
，点P的坐标为（0，
）.
综上所述所求点P的坐标为（0，
）或（0，
）
(4) 作图痕迹如答图25-2所示.
由图可知，满足条件的点有
、
、
、
，共4个可能的位置
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
重合），
的取值范围是 ．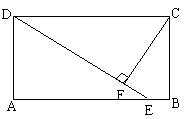
，要使
，请你增加一个条件是 ．（只需要填一个你认为合适的条件）
的两个实数根，不解方程，求下列代数式的值。
）（
） （2）
