题目内容
19．下列运算中，正确的是（ ）| A． | 3a+2b=5ab | B． | 2a3+3a2=5a5 | C． | 3a2b-3ba2=0 | D． | 5a2-4a2=1 |
分析 先根据同类项的概念进行判断是否是同类项，然后根据合并同类项的法则，即系数相加作为系数，字母和字母的指数不变计算进行判断．
解答 解：A、3a和2b不是同类项，不能合并，A错误；
B、2a3和3a2不是同类项，不能合并，B错误；
C、3a2b-3ba2=0，C正确；
D、5a2-4a2=a2，D错误，
故选：C．
点评 本题主要考查的是同类项的概念和合并同类项的法则，掌握合并同类项的法则：系数相加作为系数，字母和字母的指数不变．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
9．
将如图所示的几何图形，绕直线l旋转一周得到的立体图形（ ）
将如图所示的几何图形，绕直线l旋转一周得到的立体图形（ ）| A． |  | B． |  | C． |  | D． |  |
10．
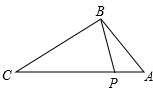如图，点P在△ABC的边AC上，要判断△ABP∽△ACB，添加一个条件，不正确的是（ ）
如图，点P在△ABC的边AC上，要判断△ABP∽△ACB，添加一个条件，不正确的是（ ）| A． | ∠ABP=∠C | B． | ∠APB=∠ABC | C． | $\frac{AP}{AB}$=$\frac{AB}{AC}$ | D． | $\frac{AB}{BP}$=$\frac{AC}{CB}$ |
7．
如图是二次函数y=ax2+bx+c的图象，下列结论：
①二次三项式ax2+bx+c的最大值为4；
②4a+2b+c＜0；
③一元二次方程ax2+bx+c=1的两根之和为-1；
④使y≤3成立的x的取值范围是x≥0．
其中正确的个数有（ ）
如图是二次函数y=ax2+bx+c的图象，下列结论：①二次三项式ax2+bx+c的最大值为4；
②4a+2b+c＜0；
③一元二次方程ax2+bx+c=1的两根之和为-1；
④使y≤3成立的x的取值范围是x≥0．
其中正确的个数有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
11．下列运算正确（ ）
| A． | a•a5=a5 | B． | a7÷a5=a3 | C． | （2a）3=6a3 | D． | 10ab3÷（-5ab）=-2b2 |
已知△ABC的顶点A、B、C在格点上，按下列要求在网格中画图．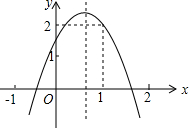
如图，二次函数y=ax2+bx+c（a≠0）的图象经过点A（1，2），与x轴交点的横坐标分别为为x1，x2，其中-1＜x1＜0，1＜x2＜2，下列结论：①4a+2b+c＜0，②2a+b＜0，③b2+8a＞4ac，④a＞-1，其中结论正确的有（ ）