题目内容
 在三行三列的方格棋盘上沿骰子的某条棱翻动骰子(相对面上分别标有1点和6点,2点和5点,3点和4点).开始时,骰子如图1所示摆放,朝上的点数是2,最后翻动到如图2所示位置.现要求翻动次数最少,则最后骰子朝上的点数为2的概率为
在三行三列的方格棋盘上沿骰子的某条棱翻动骰子(相对面上分别标有1点和6点,2点和5点,3点和4点).开始时,骰子如图1所示摆放,朝上的点数是2,最后翻动到如图2所示位置.现要求翻动次数最少,则最后骰子朝上的点数为2的概率为考点:概率公式
专题:
分析:根据已知中三行三列的方格棋盘上沿骰子的某条棱翻动骰子,我们模拟骰子的翻动过程,我们可以得到最后骰子朝上的点数所有的可能性及满足条件(即点数为2)的基本事件个数,代入古典概型公式即可得到答案.
解答:解:计三行三列的方格棋盘的格子坐标为(a,b),
其中开始时骰子所处的位置为(1,1)
则图2所示的位置为(3,3)
则从(1,1)到(3,3)共有6种走法,
其结果分别为:2,5,1,5,3,2
故最后骰子朝上的点数为2的概率为P=
=
故答案为:
其中开始时骰子所处的位置为(1,1)
则图2所示的位置为(3,3)
则从(1,1)到(3,3)共有6种走法,
其结果分别为:2,5,1,5,3,2
故最后骰子朝上的点数为2的概率为P=
| 2 |
| 6 |
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:此题考查概率的求法的运用:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
.
| m |
| n |

练习册系列答案
相关题目
2013年元月以来,雾霾天气严重影响道路交通,影响人们的正常生活.小明连续两天了解了附近两个城市的天气情况:A城市和B城市两天中均有一天是雾霾天气.则从中任意抽取一天,两个城市都不是雾霾天气的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
下列数字中是中心对称的是( )
A、 |
B、 |
C、 |
D、 |

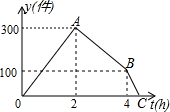 某种产品从生产流水线上下线后,需要包装人库,通常的办法是,流水线先工作一段时间,包装工人再开始工作.某次包装工人工作一段时间后,因临近下班,又抽调了一部分工人来帮忙,使包装人库的速度提高了一倍.如图是下线后待包装人库的产品数量y(件)与流水线开始工作时间t(h)的函数关系的图象.以下结论正确的有
某种产品从生产流水线上下线后,需要包装人库,通常的办法是,流水线先工作一段时间,包装工人再开始工作.某次包装工人工作一段时间后,因临近下班,又抽调了一部分工人来帮忙,使包装人库的速度提高了一倍.如图是下线后待包装人库的产品数量y(件)与流水线开始工作时间t(h)的函数关系的图象.以下结论正确的有 为了进一步丰富校园文化生活,某校举办了校园文化艺术节.小颖为了了解同学们对这次艺术节的评价,对该校的部分学生进行调查(共有很好、好、一般、不好四种评价),并绘制了如下尚不完整的统计表与扇形统计图.
为了进一步丰富校园文化生活,某校举办了校园文化艺术节.小颖为了了解同学们对这次艺术节的评价,对该校的部分学生进行调查(共有很好、好、一般、不好四种评价),并绘制了如下尚不完整的统计表与扇形统计图. 观察如图所示图形的构成规律,根据此规律,共有96个圆的是第
观察如图所示图形的构成规律,根据此规律,共有96个圆的是第