题目内容
5. 如图,AD∥BC,AC⊥AB,∠C=62°,则∠DAB的度数为( )
如图,AD∥BC,AC⊥AB,∠C=62°,则∠DAB的度数为( )| A. | 28° | B. | 30° | C. | 38° | D. | 48° |
分析 先根据三角形内角和定理,得出∠B的度数,再根据平行线的性质,即可得到∠DAB的度数.
解答 解:∵AC⊥AB,∠C=62°,
∴∠B=28°,
∵AD∥BC,
∴∠DAB=∠B=28°,
故选:A.
点评 本题主要考查了平行线的性质以及三角形内角和定理的运用,解题时注意:两直线平行,内错角相等.

练习册系列答案
相关题目
16.下列代数式中是分式的为( )
| A. | $\frac{x}{x+2}$ | B. | $\frac{{x}^{2}-2}{π}$ | C. | $\frac{4x}{7}$ | D. | $\frac{3-x}{4}$ |
20.有下列实数:$\frac{22}{7}$,-3.14159,$\sqrt{8}$,0,$\root{3}{27}$,0.$\stackrel{•}{3}\stackrel{•}{1}$,$\frac{π}{2}$,其中无理数的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.在菱形ABCD中,若AB=2,则菱形的周长为( )
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
17.已知关于x的方程ax-1=x为一元一次方程,则|a-1|一定为( )
| A. | 正 | B. | 非负 | C. | 零 | D. | 不能确定 |
14.△ABC中,D,E,F分别是边AB,BC,CA的中点,且DE=3,EF=5,DF=4,则△ABC是( )三角形.
| A. | 锐角 | B. | 直角 | ||
| C. | 钝角 | D. | 以上三种都有可能 |
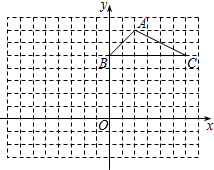 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标系,
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标系,