题目内容
6.若关于x的方程$\frac{2}{x-3}$+$\frac{x-m}{3-x}$=1无解,求m的值.分析 先将分式方程转化为整式方程,然后求得整式方程的解,最后根据分式方程无解可求得m的值.
解答 解:方程两边同时乘以(x-3)得:2-(x-m)=x-3.
解得:x=$\frac{5+m}{2}$.
∵原方程无解,
∴x=$\frac{5+m}{2}$是原方程的增根.
∴$\frac{5+m}{2}$=3.
解得:m=1.
点评 本题主要考查的是分式方程的解,根据分式方程无解得到x=3是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.下列方程中,是一元一次方程的是( )
| A. | x2-4x=3 | B. | 2x=0 | C. | x+2y=1 | D. | $x-1=\frac{1}{x}$ |
17.x表示一个一位数,y表示一个两位数,如果将x放在y的左边,则得到一个三位( )
| A. | x+y | B. | 10x+y | C. | 10y+x | D. | 100x+y |
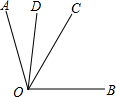 如图,OC是∠AOB的平分线,OD是∠AOC的平分线,且∠COD=25°,则∠AOD=25°,∠BOC=50°,∠AOB=100°.
如图,OC是∠AOB的平分线,OD是∠AOC的平分线,且∠COD=25°,则∠AOD=25°,∠BOC=50°,∠AOB=100°.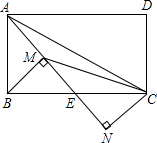 在矩形ABCD中,AD=$\sqrt{2}$AB,E为BC边的中点,过B、C两点分别作AE的垂线,M、N为垂足,连接CM、AC,则下列结论:
在矩形ABCD中,AD=$\sqrt{2}$AB,E为BC边的中点,过B、C两点分别作AE的垂线,M、N为垂足,连接CM、AC,则下列结论: