题目内容
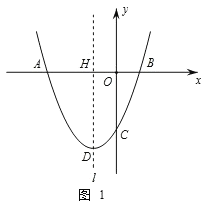
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左边),与
的左边),与![]() 轴交于
轴交于![]() 点,点
点,点![]() 是抛物线的顶点.
是抛物线的顶点.
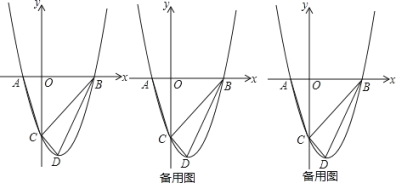
(1)求![]() 、
、![]() 、
、![]() 三点的坐标;
三点的坐标;
(2)连接![]() ,
,![]() ,
,![]() ,若点
,若点![]() 为抛物线上一动点,设点
为抛物线上一动点,设点![]() 的横坐标为
的横坐标为![]() ,当
,当![]() 时,求
时,求![]() 的值(点
的值(点![]() 不与点
不与点![]() 重合);
重合);
(3)连接![]() ,将
,将![]() 沿
沿![]() 轴正方向平移,设移动距离为
轴正方向平移,设移动距离为![]() ,当点
,当点![]() 和点
和点![]() 重合时,停止运动,设运动过程中
重合时,停止运动,设运动过程中![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() ,请直接写出
,请直接写出![]() 与
与![]() 之间的函数关系式,并写出相应自变量
之间的函数关系式,并写出相应自变量![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() 的值为
的值为![]() ,
,![]() ,2;(3)
,2;(3)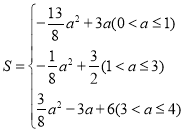
【解析】
(1)令y=0,解方程即可求得A、B的坐标,令x=0,即可求得C的坐标,把解析式化成顶点式即可求得顶点坐标;
(2)根据待定系数法求得直线BC的解析式,过点D作DE∥y轴,交BC于点E,则xD=1=xE,求得yE=2,DE=2,进而得出S△BCD=S△BED+S△CDE=![]() ×2×1+
×2×1+![]() ×2×2=3,然后分两种情况分别讨论求得即可;
×2×2=3,然后分两种情况分别讨论求得即可;
(3)分三种情况:①当0<a≤1时,根据S=S△AOCS△A′OES△FGC′即可求得;②当1<a≤3时,如图4,根据S=S△AOCS△FGC′即可求得;③当3<a≤4时,如图5,S=![]() (4a)×
(4a)×![]() (4a),故可求解.
(4a),故可求解.
解:(1)当![]() 时,
时,![]() ,
,
解得![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ;
;
(2)设![]() :
:![]()
将![]() ,
,![]() 代入得:
代入得:![]() 解得
解得![]() ,
,
∴直线![]() 为
为![]() ,
,
过点![]() 作
作![]() 轴,交
轴,交![]() 于点
于点![]() ,
,
∵![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,
过点![]() 作
作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,
,
设![]() ,
,![]()
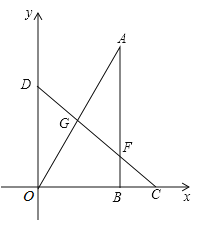
①当![]() 是
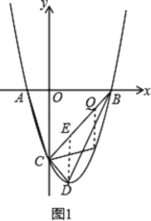
是![]() 下方抛物线上一点时,如图1,
下方抛物线上一点时,如图1,
∴![]() .
.
∴![]() (舍),
(舍),![]() ,
,
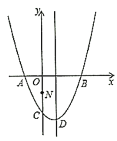
②当![]() 是
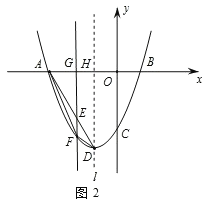
是![]() 上方抛物线上一点时,如图2,
上方抛物线上一点时,如图2,
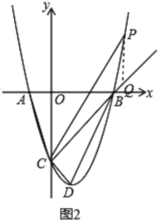
![]() ,
,
解得![]() ,
,![]() ,
,
综上:![]() 的值为
的值为![]() ,
,![]() ,2;
,2;
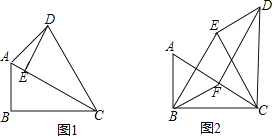
(3)①当0<a≤1时,如图3,
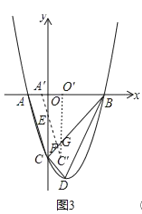
∵OA′=1a,O′C′=OC=3,
∵OE∥O’C
∴△A’OE∽△A’O’C’
∴![]()
即![]() ,
,
∴OE=33a,
∴CE=3a,
∵O’G∥OC
∴△BO’G∽△BOC
∴![]() ,
,
即![]() ,
,
∴O′G=3a,
∴GC′=a,
∵![]() ,
,
∴△FC′G边C′G上的高为![]() a,
a,
∴S=S△AOCS△A′OES△FGC′=![]() ×1×3
×1×3![]() (1a)×(/span>33a)
(1a)×(/span>33a)![]() a×
a×![]() a=
a=![]() a2+3a;
a2+3a;
②当1<a≤3时,如图4,
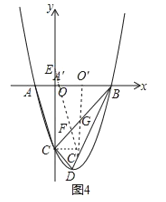
∵GC′=a,△FC′G边C′G上的高为![]() a,
a,
∴S=S△AOCS△FGC′=![]() ×1×3
×1×3![]() a×
a×![]() a=
a=![]() ;
;
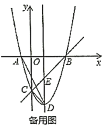
③当3<a≤4时,如图5,
∵A′B=4a,CC′=a,
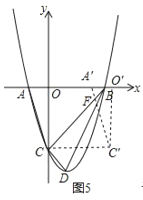
设△A′FB边A′B上的高为h,则△CFC′边CC′的高为3h,
∵△A′FB∽△C′FC,
∴![]() ,解得h=
,解得h=![]() (4a),
(4a),
∴S=![]() (4a)×
(4a)×![]() (4a)=
(4a)=![]() ;
;
综上, .
.