题目内容
如图,A,B是⊙O上的两个定点,P是⊙O上的动点(P不与A,B重合),我们称∠APB是⊙O上关于A、B的滑动角

(1)已知∠APB是⊙O上关于点A、B的滑动角,
①若AB是⊙O的直径,则∠APB= °;
②若⊙O的半径是1,AB= ,求∠APB的度数;
,求∠APB的度数;
(2)已知O2是⊙O1外一点,以O2为圆心作一个圆与⊙O1相交于A、B两点,∠APB是⊙O1上关于点A、B的滑动角,直线PA、PB分别交⊙O2于M、N(点M与点A、点N与点B均不重合),连接AN,试探索∠APB与∠MAN、∠ANB之间的数量关系,直接写出结论.
(1) ①90°②∠APB=135°
(2)∠APB=∠MAN-∠ANB;∠APB=∠MAN+∠ANB-180°;
∠APB=180°-∠MAN-∠ANB;∠APB=∠MAN+∠ANB
【解析】
试题分析:(1)①90°
②如图,连接AB、OA、OB.
在△AOB中,∵OA=OB=1.AB= ,∴OA2+OB2=AB2
,∴OA2+OB2=AB2
∴∠AOB=90°。
当点P在优弧 AB 上时(如图1),∠APB=  ∠AOB=45°;
∠AOB=45°;

当点P在劣弧 AB 上时(如图2),

∠APB=  (360°-∠AOB)=135°。
(360°-∠AOB)=135°。
(2)根据点P在⊙O1上的位置分为以下四种情况.
第一种情况:点P在⊙O2外,且点A在点P与点M之间,点B在点P与点N之间,如图3,

∵∠MAN=∠APB+∠ANB,
∴∠APB=∠MAN-∠ANB。
第二种情况:点P在⊙O2外,且点A在点P与点M之间,点N在点P与点B之间,如图4,

∵∠MAN=∠APB+∠ANP=∠APB+(180°-∠ANB),
∴∠APB=∠MAN+∠ANB-180°。
第三种情况:点P在⊙O2外,且点M在点P与点A之间,点B在点P与点N之间,如图5,

∵∠APB+∠ANB+∠MAN=180°,
∴∠APB=180°-∠MAN-∠ANB。
第四种情况:点P在⊙O2内,如图6,

∠APB=∠MAN+∠ANB。
考点:圆周角定理;勾股定理逆定理;三角形内角和定理和外角性质
点评:难度中等,关键在于分类讨论,区分点P在优弧和劣弧上两种情况讨论。

 如图,A、D是⊙O上的两个点,BC是直径,若∠D=35°,则∠OAC等于( )
如图,A、D是⊙O上的两个点,BC是直径,若∠D=35°,则∠OAC等于( )| A、65° | B、35° | C、70° | D、55° |
 如图,A、B是⊙O上的两点,AC是⊙O的切线,∠OBA=75°,⊙O的半径为1,则OC的长等于( )
如图,A、B是⊙O上的两点,AC是⊙O的切线,∠OBA=75°,⊙O的半径为1,则OC的长等于( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 20、已知:如图,E、F是AB上的两点,AE=BF,AC∥BD,∠C=∠D.求证:CF=DE.
20、已知:如图,E、F是AB上的两点,AE=BF,AC∥BD,∠C=∠D.求证:CF=DE. (2012•南京)如图,A、B是⊙O上的两个定点,P是⊙O上的动点(P不与A、B重合)、我们称∠APB是⊙O上关于点A、B的滑动角.
(2012•南京)如图,A、B是⊙O上的两个定点,P是⊙O上的动点(P不与A、B重合)、我们称∠APB是⊙O上关于点A、B的滑动角.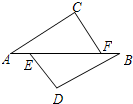 已知:如图,E、F是AB上的两点,AC=BD,AC∥BD,∠C=∠D;
已知:如图,E、F是AB上的两点,AC=BD,AC∥BD,∠C=∠D;