题目内容
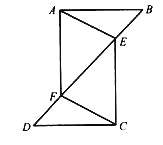
【题目】如图,![]() ,垂足为
,垂足为![]() ,垂足为B,E为
,垂足为B,E为![]() 的中点,
的中点,![]() .
.
(1)求证:![]() .
.
(2)有同学认为![]() 是线段
是线段![]() 的垂直平分线,你认为对吗?说说你的理由;
的垂直平分线,你认为对吗?说说你的理由;
(3)若![]() ,求
,求![]() 的度数.
的度数.

【答案】(1)详情见解析;(2)对,理由见解析;(3)50°
【解析】
(1)首先根据题意证明∠ADB=∠BEC,然后利用“AAS”证明△ADB与△BEC全等,最后利用全等三角形性质进一步证明即可;
(2)根据E是AB的中点可知AE=BE,从而得出AE=AD,然后根据AB=BC得出∠BAC=∠BCA,据此结合题意进一步证明△ADC△AEC,由此得出DC=CE,从而得出C点在线段DE的垂直平分线上,最后进一步证明出A点在线段DE的垂直平分线上,由此即可得出结论;
(3)首先利用全等三角形性质得出DB=CE,结合题意进一步得出∠CBD=∠BCD,据此求出∠CBD的度数,然后进一步求解即可.
(1)∵BD⊥EC,DA⊥AB,
∴∠BEC+∠DBA=90°,∠DBA+∠ADB=90°,
∴∠ADB=∠BEC,
在△ADB与△BEC中,
∵∠ADB=∠BEC,∠DAB=∠EBC,AB=BC,
∴△ADB△BEC(AAS),
∴BE=AD;
(2)对的,![]() 是线段
是线段![]() 的垂直平分线,理由如下:
的垂直平分线,理由如下:
∵E是AB中点,
∴AE=BE,
∵BE=AD,
∴AE=AD,
∵AB=BC,
∴∠BAC=∠BCA,
∵DA⊥AB,CB⊥AB,
∴AD∥BC,
∴∠DAC=∠BCA,
∴∠BAC=∠DAC,
在△ADC与△AEC中,
∵AD=AE,∠DAC=∠EAC,AC=AC,
∴△ADC△AEC(SAS),
∴DC=CE,
∴C点在线段DE的垂直平分线上,
∵AD=AE,
∴A点在线段DE的垂直平分线上,
∴AC垂直平分DE;
(3)∵AC是线段DE的垂直平分线,
∴CD=CE,
∵△ADB△BEC(AAS),
∴DB=CE,
∴CD=BD,
∴∠CBD=∠BCD,
∵∠ABD=25°,
∴∠CBD=90°25°=65°,
∴∠BDC=180°2∠CBD=50°.