题目内容
1.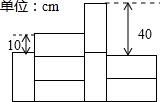 如图所示是由截面为同一种矩形的墙砖粘贴的部分墙面,其中三块横放的墙砖比一块竖放的墙砖高10cm,两块横放的墙砖比两块竖放的墙砖低40cm,则每块墙砖的截面面积是( )
如图所示是由截面为同一种矩形的墙砖粘贴的部分墙面,其中三块横放的墙砖比一块竖放的墙砖高10cm,两块横放的墙砖比两块竖放的墙砖低40cm,则每块墙砖的截面面积是( )| A. | 425cm2 | B. | 525cm2 | C. | 600cm2 | D. | 800cm2 |
分析 设每块墙砖的长为xcm,宽为ycm,根据“三块横放的墙砖比一块竖放的墙砖高10cm,两块横放的墙砖比两块竖放的墙砖低40cm”列方程组求解可得.
解答 解:设每块墙砖的长为xcm,宽为ycm,
根据题意得:$\left\{\begin{array}{l}{x+10=3y}\\{2x=2y+40}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=35}\\{y=15}\end{array}\right.$,
则每块墙砖的截面面积是35×15=525cm2,
故选:B.
点评 本题主要考查二元一次方程组的应用,理解题意找到题目蕴含的相等关系列方程组是解题的关键.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
14.一次函数y=ax+b图象经过(0,2)和(3,0)两点,方程ax+b=0的解是( )
| A. | -2 | B. | 3 | C. | -2和3 | D. | 0 |
13.下列计算正确的是( )
| A. | 3x2y-2x2y=x2y | B. | 7a+a=7a2 | C. | 5y-3y=2 | D. | 3a+2b=5ab |
11.某商品每件的标价是660元,按标价的八折销售时,仍可获利10%,则这种商品每件的进价为( )元.
| A. | 480 | B. | 490 | C. | 520 | D. | 540 |
 如图,直线AB、CD相交于点O,OE平分∠AOD,OF垂直于CD垂足为O,∠1+∠2=∠3,求∠1、∠2、∠3的度数.
如图,直线AB、CD相交于点O,OE平分∠AOD,OF垂直于CD垂足为O,∠1+∠2=∠3,求∠1、∠2、∠3的度数. 如图,CD是⊙O的直径,线段AB过圆心O,且OA=OB=$\sqrt{5}$,CD=2,连接AC、AD、BD、BC、AD、CB分别交⊙O于E、F.当AC与⊙O相切时,问四边形CEDF是何种特殊四边形?请证明你的结论.
如图,CD是⊙O的直径,线段AB过圆心O,且OA=OB=$\sqrt{5}$,CD=2,连接AC、AD、BD、BC、AD、CB分别交⊙O于E、F.当AC与⊙O相切时,问四边形CEDF是何种特殊四边形?请证明你的结论.