题目内容
已知|m-3|+(n+2)2=0,则nm的值为 .
考点:非负数的性质:偶次方,非负数的性质:绝对值
专题:
分析:先根据非负数的性质求出m、n的值,进而可得出结论.
解答:解:∵|m-3|+(n+2)2=0,
∴m-3=0,n+2=0,解得m=3,n=-2,
∴nm=(-2)3=-8.
故答案为:-8.
∴m-3=0,n+2=0,解得m=3,n=-2,
∴nm=(-2)3=-8.
故答案为:-8.
点评:本题考查的是非负数的性质,熟知一个数的偶次方或绝对值均为非负数是解答此题的关键.

练习册系列答案
相关题目
数据1、2、5、3、5、3、5的众数是( )
| A、1 | B、2 | C、3 | D、5 |
一个多边形的每一个内角都等于140°,则它的边数是( )
| A、7 | B、8 | C、9 | D、10 |
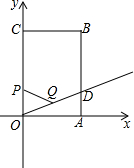 已知如图,矩形OABC在平面直角坐标系中,OA=
已知如图,矩形OABC在平面直角坐标系中,OA= 如图,点D在Rt△ABC的斜边AB上,AD=7,DB=11,∠CDB=2∠B,则CD=
如图,点D在Rt△ABC的斜边AB上,AD=7,DB=11,∠CDB=2∠B,则CD=