题目内容
【题目】在四边形ABCD中,BD平分∠ABC.
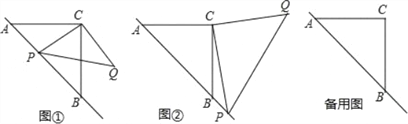
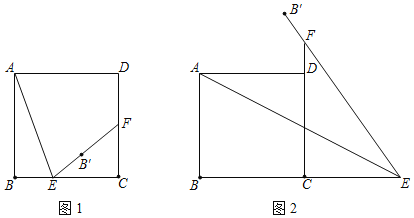
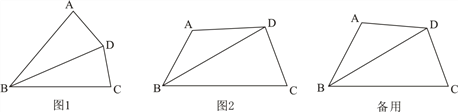
(1)如图1,若∠A=∠BDC,求证:BD2=AB·BC;
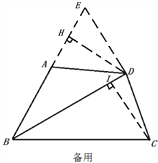
(2)如图2,∠A>90°,∠BAD+∠BDC=180°,
① 若∠ABC=60°,AB=![]() ,BC=4,求
,BC=4,求![]() ;
;
② 若BC=2n,CD=n,BD=8,则AB的长为________.
【答案】(1)证明见解析(2)![]() (3)
(3)![]()
【解析】(1)通过证明△ABD∽△DBC即可得到结论.
(2)延长BA到E,使DE=DA,作DH⊥AE于点H,得到∠EAD=∠E.可证明△EBD∽△DBC,由相似三角形的性质即可得到BD2=EB·BC.
设DH=x,则BH=![]() ,AH=HE=
,AH=HE=![]() ,BE=BH+EH=
,BE=BH+EH=![]() ,故
,故![]() ,解方程得到x的值,即可得到BD的值.由相似三角形的
,解方程得到x的值,即可得到BD的值.由相似三角形的
∵△EBD∽△DBC,
∴![]() .
.
(3)延长BA到E,使DE=DA,作DH⊥AE于点H,
∴∠EAD=∠E.
∵∠EAD+∠BAD=180°,∠BAD+∠BDC=180°,
∴∠BDC=∠EAD=∠E.
∵∠ABD=∠DBC,∴△EBD∽△DBC,∴![]() ,∴BD2=EB·BC,
,∴BD2=EB·BC,![]() ,∴BE=
,∴BE=![]() ,ED=AD=4.
,ED=AD=4.
设AH=y,HD=h,则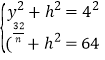 ,解得:
,解得:![]() ,∴AB=BE-2y=
,∴AB=BE-2y=![]() =
=![]() .
.
(1) ∵BD平分∠ABC,∴∠ABD=∠DBC,
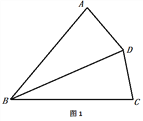
∵∠A=∠BDC,∴△ABD∽△DBC,
∴![]() ,∴BD2=AB·BC,
,∴BD2=AB·BC,
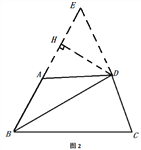
(2)延长BA到E,使DE=DA,作DH⊥AE于点H,
∴∠EAD=∠E.
∵∠EAD+∠BAD=180°,∠BAD+∠BDC=180°,
∴∠BDC=∠EAD=∠E.
∵∠ABD=∠DBC,∴△EBD∽△DBC,![]() ,∴BD2=EB·BC.
,∴BD2=EB·BC.
设DH=x,则BH=![]() ,AH=HE=
,AH=HE=![]() ,
,
∴BE=BH+EH=![]() ,∴
,∴![]() ,
,
解得:![]() .
.
∵AH=HE=![]() >0,∴
>0,∴![]() ,∴
,∴![]() ,
,
∴BD=![]() .
.
∵△EBD∽△DBC,
∴![]() .
.
(3)延长BA到E,使DE=DA,作DH⊥AE于点H,
∴∠EAD=∠E.
∵∠EAD+∠BAD=180°,∠BAD+∠BDC=180°,
∴∠BDC=∠EAD=∠E.
∵∠ABD=∠DBC,∴△EBD∽△DBC,∴![]() ,∴BD2=EB·BC,
,∴BD2=EB·BC,![]() ,∴BE=
,∴BE=![]() ,ED=AD=4.
,ED=AD=4.
设AH=y,HD=h,则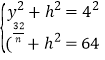 ,解得:
,解得:![]() ,∴AB=BE-2y=
,∴AB=BE-2y=![]() =
=![]() .
.


【题目】为了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计表.调查结果统计表
组别 | 分组(单位:元) | 人数 |
|
| 4 |
|
| 16 |
|
|
|
|
|
|
|
| 2 |
调查结果扇形统计图
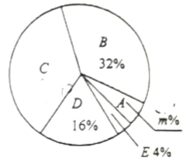
请根据以上图表,解答下列问题:
(1)这次被调查的同学共有 人, ,
![]()
![]() ;
;
(2)求扇形统计图中扇形![]() 的圆心角的度数;
的圆心角的度数;
(3)若该校共有学生1000人,请估计每月零花钱的数额![]() 在
在![]() 范围的人数.
范围的人数.