题目内容
将边长为1的正方形按下列方式排列：
如果第n个图形共排列有132个边长为1的正方形，则n=
如果第n个图形共排列有132个边长为1的正方形，则n=
11
11
．分析：首先发现规律，然后利用规律n（n+1）解答．
解答：解：第1个图形有1×2=2个边长为1的正方形；
第2个图形有2×3=6个边长为1的正方形；
第3个图形有3×4=12个边长为1的正方形；
…
第n个图形有n（n+1）个边长为1的正方形；
∴n（n+1）=132
解得：n=11
故答案为：11．
第2个图形有2×3=6个边长为1的正方形；
第3个图形有3×4=12个边长为1的正方形；
…
第n个图形有n（n+1）个边长为1的正方形；
∴n（n+1）=132
解得：n=11
故答案为：11．
点评：本题考查了图形的变化类问题，发现规律n（n+1）是解决本类题目的关键．
练习册系列答案
同步练习河南大学出版社系列答案
同步练习西南大学出版社系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目
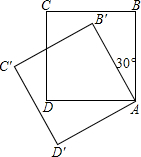如图，将边长为1的正方形ABCD绕A点按逆时针方向旋转30°，至正方形AB′C′D′，则旋转前后正方形重叠部分的面积是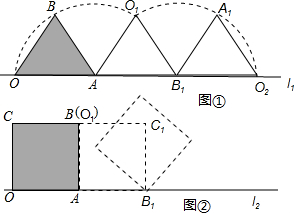
将边长为3厘米的正方形ABCD绕点C按顺时针方向旋转30°，得到正方形EFCG，EF交AD于H，则DH的长是多少？
将边长为1的正方形ABCD绕A点按逆时针方向旋转60°，至正方形AB′C′D′，则旋转前后两个正方形重叠部分的面积为