题目内容
16.已知∠ABC=30°,边BC上有一点O,BO=2,⊙O的半径r为多少时,⊙O与AB相交、相切、相离?分析 作OD⊥AB于D,则∠ODB=90°,由含30°角的直角三角形的性质得出OD=1,由d与r的关系,即可得出结果.
解答 解:作OD⊥AB于D,如图所示:
则∠ODB=90°,
∵∠ABC=30°,
∴OD=$\frac{1}{2}$B1,
∴当0<r<1时,⊙O与AB相离;
当r=1时,⊙O与AB相切;
当r>1时,⊙O与AB相交.
点评 本题考查了直线与圆的位置关系、含30°角的直角三角形的性质;熟记d与r的数量关系与直线与圆的位置关系,由含30°角的直角三角形的性质求出OD是解决问题的关键.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 奇奇妈妈买了一块正方形地毯,地毯上有“※”组成的图案,观察局部有如此规律:奇奇数※个数的方法是用“L”来划分,从右上角的1个开始,一层一层往外数,第一层1个,第二层3个,第三层5个…,这样她发现了连续奇数求和的方法.
奇奇妈妈买了一块正方形地毯,地毯上有“※”组成的图案,观察局部有如此规律:奇奇数※个数的方法是用“L”来划分,从右上角的1个开始,一层一层往外数,第一层1个,第二层3个,第三层5个…,这样她发现了连续奇数求和的方法.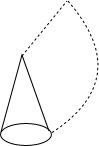 (1)已知圆锥的底面半径为2cm,母线长为4cm,求圆锥的表面积;
(1)已知圆锥的底面半径为2cm,母线长为4cm,求圆锥的表面积;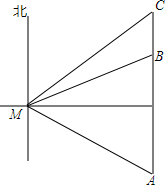 如图,在小岛M处测得一艘渔船位于南偏东45°方向A处,该渔船从南向正北方向行驶一段距离后,到达位于小岛北偏东60°方向的B处,又航行了半小时到达C处,此时渔船在小岛的东北方向,渔船的速度为20海里/小时.
如图,在小岛M处测得一艘渔船位于南偏东45°方向A处,该渔船从南向正北方向行驶一段距离后,到达位于小岛北偏东60°方向的B处,又航行了半小时到达C处,此时渔船在小岛的东北方向,渔船的速度为20海里/小时.