题目内容
 如图,AB∥CD,直线l分别交AB、CD于点E、F,EG平分∠BEF,若∠EFG=50°,则∠EGD的度数是
如图,AB∥CD,直线l分别交AB、CD于点E、F,EG平分∠BEF,若∠EFG=50°,则∠EGD的度数是
- A.115°
- B.125°
- C.130°
- D.100°
A
分析:由AB∥CD,根据两直线平行,同旁内角互补,即可求得∠BEF的度数,又由EG平分∠BEF,即可得∠GEF的度数,然后利用三角形外角的性质,即可求得∠EGD的度数.
解答:∵AB∥CD,
∴∠BEF+∠EFG=180°,
∵∠EFG=50°,
∴∠BEF=130°,
∵EG平分∠BEF,
∴∠GEF= ∠BEF=65°,
∠BEF=65°,
∴∠EGD=∠GEF+∠EFG=65°+50°=115°.
故选A.
点评:此题考查了平行线的性质、角平分线的定义以及三角形外角的性质.此题难度不大,解题的关键是掌握两直线平行,同旁内角互补定理的应用,掌握数形结合思想的应用.
分析:由AB∥CD,根据两直线平行,同旁内角互补,即可求得∠BEF的度数,又由EG平分∠BEF,即可得∠GEF的度数,然后利用三角形外角的性质,即可求得∠EGD的度数.
解答:∵AB∥CD,
∴∠BEF+∠EFG=180°,
∵∠EFG=50°,
∴∠BEF=130°,
∵EG平分∠BEF,
∴∠GEF=
 ∠BEF=65°,
∠BEF=65°,∴∠EGD=∠GEF+∠EFG=65°+50°=115°.
故选A.
点评:此题考查了平行线的性质、角平分线的定义以及三角形外角的性质.此题难度不大,解题的关键是掌握两直线平行,同旁内角互补定理的应用,掌握数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
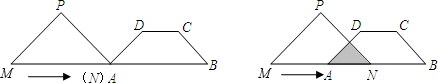
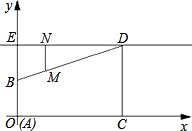 横坐标为x,纵坐标为y.
横坐标为x,纵坐标为y. 如图,将网格中的三条线段AB、CD、EF沿网格线(水平和铅直方向)平移,使它们首尾相接构成三角形,至少需要移动
如图,将网格中的三条线段AB、CD、EF沿网格线(水平和铅直方向)平移,使它们首尾相接构成三角形,至少需要移动
