题目内容
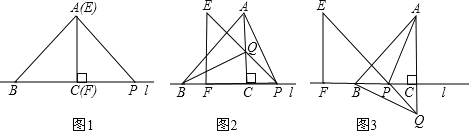
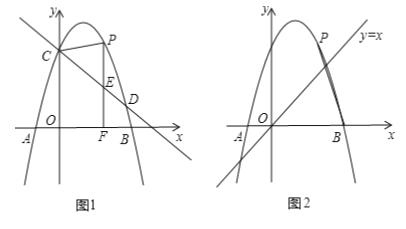
【题目】在平面直角坐标系xOy中,直线y=x与双曲线y=![]() (k>0,x>0)交于点A.过点A作AC⊥x轴于点C,过双曲线上另一点B作BD⊥x轴于点D,作BE⊥AC于点E,连接AB.若OD=3OC,则tan∠ABE=______.
(k>0,x>0)交于点A.过点A作AC⊥x轴于点C,过双曲线上另一点B作BD⊥x轴于点D,作BE⊥AC于点E,连接AB.若OD=3OC,则tan∠ABE=______.
【答案】![]()
【解析】
由直线y=x过点A,可设A(a,a),根据反比例函数图象上点的坐标特征以及已知条件得到B(3a,![]() ).然后解直角△ABE,根据正切函数的定义即可求出tan∠ABE的值.
).然后解直角△ABE,根据正切函数的定义即可求出tan∠ABE的值.
解:如图.∵直线y=x过点A,
∴可设A(a,a),
∵AC⊥x轴于点C,BD⊥x轴于点D,OD=3OC,
∴B点横坐标为3a.
∵双曲线y=![]() (k>0,x>0)过点A、点B,
(k>0,x>0)过点A、点B,
∴B点纵坐标为![]() ,
,
∴B(3a,![]() ).
).
在直角△ABE中,∵∠AEB=90°,BE=3aa=2a,AE=a![]() ,
,
∴tan∠ABE= ,
,
故答案为![]() .
.


练习册系列答案
相关题目
【题目】某村启动“脱贫攻坚”项目,根据当地的地理条件,要在一座高为1000m的上种植一种经济作物.农业技术人员在种植前进行了主要相关因素的调查统计,结果如下:
①这座山的山脚下温度约为22°C,山高h(单位:m)每增加100m,温度T(单位:°C)下降约0.5°C;
②该作物的种植成活率p受温度T影响,且在19°C时达到最大.大致如表:
温度T°C | 21 | 20.5 | 20 | 19.5 | 19 | 18.5 | 18 | 17.5 |
种植成活率p | 90% | 92% | 94% | 96% | 98% | 96% | 94% | 92% |
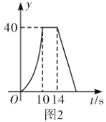
③该作物在这座山上的种植量w受山高h影响,大致如图1:
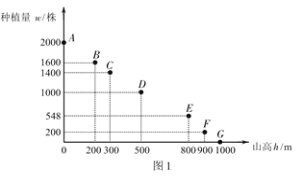
(1)求T关于h的函数解析式,并求T的最小值;
(2)若要求该作物种植成活率p不低于92%,根据上述统计结果,山高h为多少米时该作物的成活量最大?请说明理由.