Question

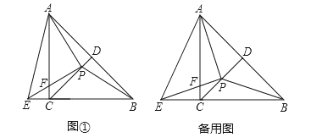
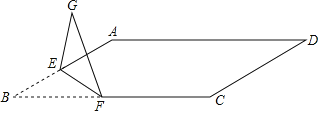
【题目】如图，在ABCD中，AB＝6，BC＝6，∠D＝30°，点E是AB边的中点，点F是BC边上一动点，将△BEF移沿直线EF折叠，得到△GEF，当FG∥AC时，BF的长为_____．

Answer 1

【答案】或

【解析】

由平行四边形的性质得出∠B＝∠D＝30°，CD＝AB＝6，AD＝BC＝6，作CH⊥AD于H，则CH＝CD＝3，DH＝CH＝3＝AD，得出AH＝DH，由线段垂直平分线的性质得出CA＝CD＝AB＝6，由等腰三角形的性质得出∠ACB＝∠B＝30°，由平行线的性质得出∠BFG＝∠ACB＝30°，分两种情况：

①作EM⊥BF于M，在BF上截取EN＝BE＝3，则∠ENB＝∠B＝30°，由直角三角形的性质得出EM＝BE＝，BM＝NM＝EM＝，得出BN＝2BM＝3，再证出FN＝EN＝3，即可得出结果；

②作EM⊥BC于M，在BC上截取EN＝BE＝3，连接EN，则∠ENB＝∠B＝30°，得出EN∥AC，EM＝BE＝，BM＝NM＝EM＝，BN＝2BM＝3，证出FG∥EN，则∠G＝∠GEN，证出∠GEN＝∠ENB＝∠B＝∠G＝30°，推出∠BEN＝120°，得出∠BEG＝120°﹣∠GEN＝90°，由折叠的性质得∠BEF＝∠GEF＝∠BEG＝45°，证出∠NEF＝∠NFE，则FN＝EN＝3，即可得出结果．

解：∵四边形ABCD是平行四边形，

∴∠B＝∠D＝30°，CD＝AB＝6，AD＝BC＝6，

作CH⊥AD于H，

则CH＝CD＝3，DH＝CH＝3＝AD，

∴AH＝DH，

∴CA＝CD＝AB＝6，

∴∠ACB＝∠B＝30°，

∵FG∥AC，

∴∠BFG＝∠ACB＝30°，

∵点E是AB边的中点，

∴BE＝3，

分两种情况：

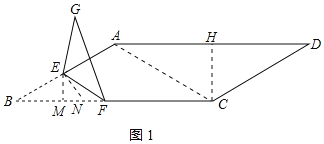
①作EM⊥BF于M，在BF上截取EN＝BE＝3，连接EN，如图1所示：

则∠ENB＝∠B＝30°，

∴EM＝BE＝，BM＝NM＝EM＝，

∴BN＝2BM＝3，

由折叠的性质得：∠BFE＝∠GFE＝15°，

∵∠NEF＝∠ENB﹣∠BFE＝15°＝∠BFE，

∴FN＝EN＝3，

∴BF＝BN+FN＝3+3；

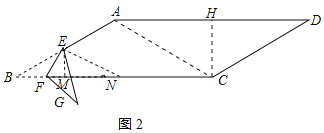
②作EM⊥BC于M，在BC上截取EN＝BE＝3，连接EN，如图2所示：

则∠ENB＝∠B＝30°，

∴EN∥AC，EM＝BE＝，BM＝NM＝EM＝，

∴BN＝2BM＝3，

∵FG∥AC，

∴FG∥EN，

∴∠G＝∠GEN，

由折叠的性质得：∠B＝∠G＝30°，

∴∠GEN＝∠ENB＝∠B＝∠G＝30°，

∵∠BEN＝180°﹣∠B﹣∠ENB＝180°﹣30°﹣30°＝120°，

∴∠BEG＝120°﹣∠GEN＝120°﹣30°＝90°，

由折叠的性质得：∠BEF＝∠GEF＝∠BEG＝45°，

∴∠NEF＝∠NEG+∠GEF＝30°+45°＝75°，∠NFE＝∠BEF+∠B＝45°+30°＝75°，∴∠NEF＝∠NFE，∴FN＝EN＝3，

∴BF＝BN﹣FN＝3﹣3；

故答案为：或．