题目内容
【题目】如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为3,OP=1,求BC的长.
【答案】
(1)证明:连接OB,如图,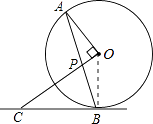
∵OP⊥OA,
∴∠AOP=90°,
∴∠A+∠APO=90°,
∵CP=CB,
∴∠CBP=∠CPB,
而∠CPB=∠APO,
∴∠APO=∠CBP,
∵OA=OB,
∴∠A=∠OBA,
∴∠OBC=∠CBP+∠OBA=∠APO+∠A=90°,
∴OB⊥BC,
∴BC是⊙O的切线
(2)解:设BC=x,则PC=x,
在Rt△OBC中,OB=3,OC=CP+OP=x+1,
∵OB2+BC2=OC2 ,
∴32+x2=(x+1)2 ,
解得x=4,
即BC的长为4
【解析】(1)要证明BC是⊙O的切线,连半径证垂直,因此连接OB,先根据垂线的定义及三角形内角和定理证明∠A+∠APO=90°,再根据对顶角相等及等腰三角形的性质证明∠APO=∠CBP,∠CBP=∠CPB,∠A=∠OBA,然后再证明∠OBC=90°,即可证得结论。
(2)根据已知设CP=CB=x,用含x的代数式表示出OC,再在Rt△OBC中,利用勾股定理建立关于x的方程,解方程求出x的值,即可得出答案。

练习册系列答案
相关题目