题目内容
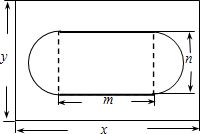 某居民小区为了美化环境,要在一块长为x,宽为y的矩形绿地上建造花坛,要求花坛所占面积不超过绿地面积的一半,小明为此设计一个如图的方案,花坛是由一个矩形和两个半圆组成的,其中m,n分别是x,y的
某居民小区为了美化环境,要在一块长为x,宽为y的矩形绿地上建造花坛,要求花坛所占面积不超过绿地面积的一半,小明为此设计一个如图的方案,花坛是由一个矩形和两个半圆组成的,其中m,n分别是x,y的| 1 |
| 2 |
| 3 |
| 2 |
分析:先表示出花坛所占面积,再表示出花坛面积减去矩形面积的一半,可得出
S矩形=0.75y2,即得出小明的设计方案符合要求.
| 1 |
| 2 |
解答:解:解法一:S花坛=mn+(
n)2π,(1分)
=
x•
y+(
×
y)2π,
=
xy+
πy2(2分);
S花坛-
S矩形=
xy+
πy2-
xy,(3分)
=
πy2-
xy,
=
πy•
x-
xy,
=(
-
)xy<0
解法二:S花坛=mn+(
n)2π(1分)
=
x•
y+(
×
y)2π
=(
+
)y2
≈0.572y2(2分)
S矩形=0.75y2(3分),
∴符合要求(5分)(此处取近似值比较扣1分)
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 4 |
| 1 |
| 16 |
S花坛-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 16 |
| 1 |
| 2 |
=
| 1 |
| 16 |
| 1 |
| 4 |
=
| 1 |
| 16 |
| 2 |
| 3 |
| 1 |
| 4 |
=(
| π |
| 24 |
| 1 |
| 4 |
解法二:S花坛=mn+(
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=(
| л |
| 16 |
| 3 |
| 8 |
≈0.572y2(2分)
| 1 |
| 2 |
∴符合要求(5分)(此处取近似值比较扣1分)
点评:本题是一道综合性的题目,考查了整式的混合运算、扇形的面积、矩形的面积等知识点,难度较大,是一道竞赛题.

练习册系列答案
相关题目
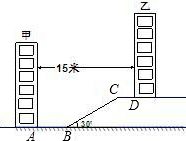 某住宅小区为了美化环境,增加绿地面积,决定在坡地上的甲楼和乙楼之间建一块斜坡草地,如图,已知两楼的水平距离为15米,距离甲楼2米(即AB=2米)开始修建坡角为30°的斜坡,斜坡的顶端距离乙楼4米(即CD=4米),求斜坡BC的长度(结果保留根号).
某住宅小区为了美化环境,增加绿地面积,决定在坡地上的甲楼和乙楼之间建一块斜坡草地,如图,已知两楼的水平距离为15米,距离甲楼2米(即AB=2米)开始修建坡角为30°的斜坡,斜坡的顶端距离乙楼4米(即CD=4米),求斜坡BC的长度(结果保留根号).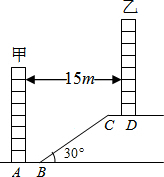 (2010•本溪一模)某住宅小区为了美化环境,增加绿地面积,决定在甲楼和乙楼之间的坡地上建一块斜坡草地为绿化带,如图,已知两楼的水平距离为15米,距离甲楼4米(即AB=4米)开始修建坡角为30°的斜坡,斜坡的顶端距离乙楼2米(即CD=2米),如果绿化带总长为10米,求绿化带的面积.(
(2010•本溪一模)某住宅小区为了美化环境,增加绿地面积,决定在甲楼和乙楼之间的坡地上建一块斜坡草地为绿化带,如图,已知两楼的水平距离为15米,距离甲楼4米(即AB=4米)开始修建坡角为30°的斜坡,斜坡的顶端距离乙楼2米(即CD=2米),如果绿化带总长为10米,求绿化带的面积.(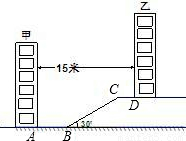
 ,若x=
,若x= y,则小明的设计方案是否符合要求?请你用方法加以说明。
y,则小明的设计方案是否符合要求?请你用方法加以说明。